Question

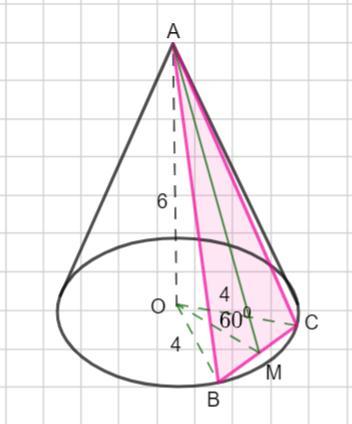
Через вершину конуса з висотою 6 і радіусом основи 4 проведена сiчна площина, яка утворює кут 60° iз площиною основи. Знайдіть площу перерізу.​

Answer 1

Ответ:

Площадь сечения равна 8√3 кв. ед.

Объяснение:

Через вершину конуса высотою 6 и радиусом основания 4 проведено секущая плоскость , которая образует угол в 60° с плоскостью основания . Найти площадь сечения.

Пусть дан конус. Через вершину конуса проведено сечение - это равнобедренный ΔАВС  . По условию высота АО =6 ед., если радиус основания равен 4, то ОВ =ОС = 4 ед.

Проведем высоту АМ  ΔАВС . Тогда АМ ⊥ВС , по теореме о трех перпендикулярах ОМ ⊥ВС  и ∠АМО =60 ° - угол , который образует сечение с плоскостью основания.

Рассмотрим ΔАОМ - прямоугольный .

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

$sin 60^{0} =\dfrac{AO }{AM} ;\\\\\dfrac{\sqrt{3} }{2} = \dfrac{6}{AM} ;\\\\AM= \dfrac{6\cdot2 }{\sqrt{3} } =\dfrac{12}{\sqrt{3} } =\dfrac{12\cdot \sqrt{3} }{\sqrt{3} \cdot \sqrt{3} } =\dfrac{12\sqrt{3} }{3} =4\sqrt{3}$

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему

$tg 60^{0} =\dfrac{AO }{OM} ;\\\\\\\sqrt{3} = \dfrac{6}{OM} ;\\\\OM= \dfrac{6 }{\sqrt{3} } =\dfrac{6\cdot \sqrt{3} }{\sqrt{3} \cdot \sqrt{3} } =\dfrac{6\sqrt{3} }{3} =2\sqrt{3}$

Рассмотрим ΔВОС - равнобедренный . ОМ - высота, а значит и медиана.

Рассмотрим ΔОМВ - прямоугольный. Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$OB^{2} =OM ^{2} +MB^{2} ;\\MB^{2}=OB^{2} -OM ^{2};\\MB = \sqrt{OB^{2} -OM ^{2}} ;\\MB =\sqrt{4^{2} -(2\sqrt{3} )^{2} } =\sqrt{16-12} =\sqrt{4} =2$

Так как ОМ  - медиана, то МВ = МС = 2 ед. Тогда ВС = 4 ед.

Найдем площадь сечения, то есть площадь треугольника, как полупроизведение стороны на высоту, проведенную к данной стороне.

$S =\dfrac{1}{2} \cdot BC \cdot AM ;\\\\S =\dfrac{1}{2} \cdot 4 \cdot 4\sqrt{3} =8\sqrt{3} .$

Значит, площадь сечения равна 8√3 кв. ед.

#SPJ1