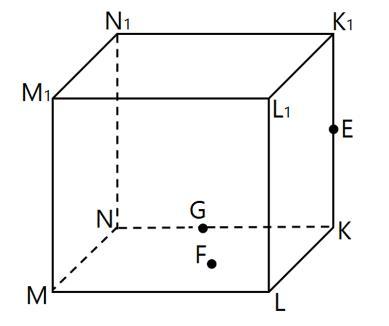
Задан прямоугольный параллелепипед MNKLM1N1K1L1. Точка E лежит на ребре KK1, точка G – на ребре NK, точка F – на нижней грани.
а) Постройте сечение параллелепипеда по трём заданным точкам E, F, G. Объясните ход построения каждого из отрезков.
б) Укажите название (вид) полученного многоугольника и заштрихуйте его внутреннюю часть.
Приложения:
Ответы
Ответ дал:
2
Ответ:
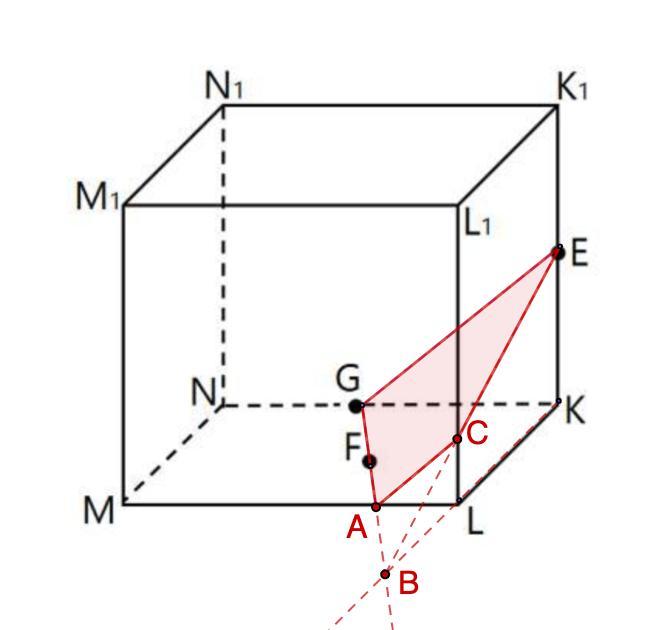
Построили сечение AGEC - трапеция.
Объяснение:
Задан прямоугольный параллелепипед MNKLM₁N₁K₁L₁. Точка E лежит на ребре KK₁, точка G – на ребре NK, точка F – на нижней грани.
а) Постройте сечение параллелепипеда по трём заданным точкам E, F, G. Объясните ход построения каждого из отрезков.
б) Укажите название (вид) полученного многоугольника и заштрихуйте его внутреннюю часть.
- Через две точки можно провести прямую линию.
- Если две плоскости пересекаются, то линия пересечения принадлежит обеим плоскостям.
1. Точки G и E лежат в одной плоскости NN₁K₁K ⇒ соединяем.
2. Точки G и F лежат в одной плоскости MNKL ⇒ соединяем.
GF ∩ ML = A
3. KL ⊂ MNKL; KL ⊂ LL₁K₁K
GA ∩ KL = B
4. Точки В и Е лежат в одной плоскости LL₁K₁K ⇒ соединяем.
5. ВЕ ∩ LL₁ = C
6. Точки A и C лежат в одной плоскости ММ₁L₁L ⇒ соединяем.
AGEC - сечение.
- Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
⇒ GE || AC ⇒ AGEC - трапеция.
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад