Question

Бісектриса прямокутника, ділить його діагональ на відрізки, що відносяться як 3:5. Знайдіть сторони прямокутника, якщо його периметр 48 см.

Answer 1

Ответ:

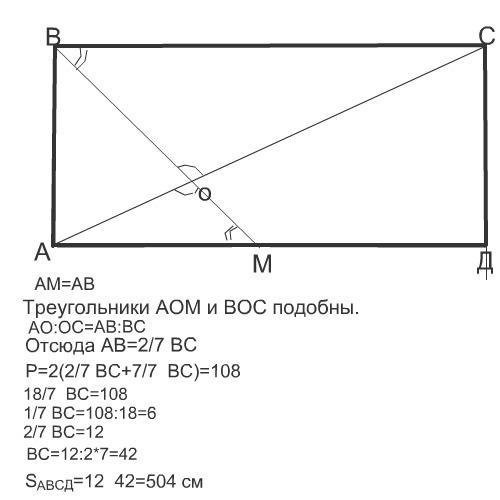
Задача на подобие треугольников.

Сделаем рисунок и рассмотрим треугольники АОМ и ВОС. Они подобны по двум углам.

Из подобия треугольников АОМ и ВОС

АО:ОС=АМ:ВС

АМ=АВ, т.к. это катеты равнобедренного прямоугольного треугольника АВМ с углами при основани ВМ=45°, поэтому

2:7=АВ:ВС

2ВС=7АВ

Периметр прямоугольника АВСД=2ВС+2АВ

Но 2 ВС=7АВ

Р=7АВ+2АВ=108 см

АВ=108:9=12 см

ВС=12·7÷2=42 см

Площадь прямоугольника равна

S=12·42=504 cм²

--------------------

В рисунке вычисления сделала немного иначе, на результат это не влияет.

Объяснение:

Answer 2

Відповідь:

AB=9 см

BC=15 см

Пояснення: