Question

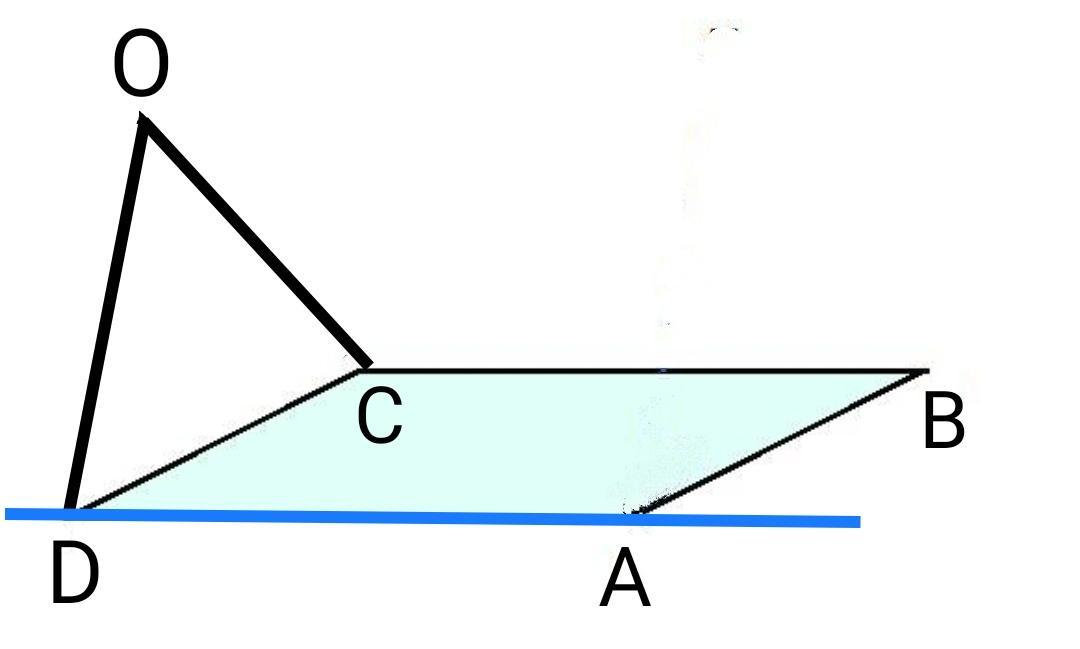
точка O не принадлежит плоскости квадрата abcd определите взаимное расположение прямой ad и плоскости DOC. Помогите решить .срочно
​

Answer 1

Ответ:

АD ∩ (DOC) = D.

Объяснение:

Прямая и плоскость могут быть параллельными,

прямая может иметь с плоскостью только одну общую точку, в этом случае она пересекает плоскость,

прямая может лежать в плоскости.

В нашем случае прямая АD и плоскость (DOC) уже имеют общую точку D, а значит они не параллельны.

По условию (DOC) ∩ (АВС) = DС.

Предположим, что прямая АD лежит в (DOC), тогда и А є (DOC), А - общая точкой плоскостей (DOC) и (АВС).

По аксиоме, если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Получили, что А є DC, а этого быть не может, т.к. стороны квадрата АВ II DC, т.е. общих точек не имеют.

Наше предположение неверное, остаётся, что АD ∩ (DOC) = D.