Question

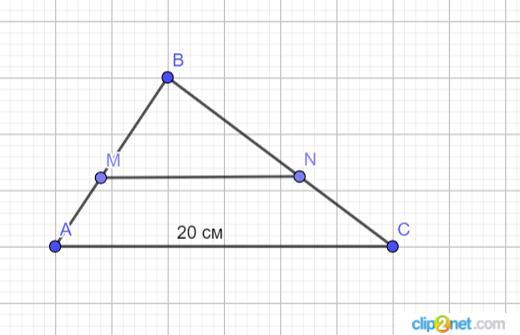
Користуючись рисунком, знайдіть MN, якщо АС = 20 см, MN ∥ AC, а точка М ділить сторону АВ трикутника АВС у відношенні АВ : BМ = 5 : 3.

Answer 1

Ответ:

MN = 12 см

Объяснение:

Если MN ∥ AC, то мы имеем два подобных треугольника.

( MN ∥ AC  ⇒   ∠BMN = ∠BAC  как соответственные.

Аналогично  ∠BNM = ∠BCA

Треугольники подобны по первому признаку подобия.)

Отношение сходственных сторон подобных треугольников попарно равно коэффициенту подобия.

У нас есть коэффициент подобия  АВ : BМ = 5 : 3,

следовательно АС : MN = 5 : 3, и АС = 20см.

Используем основное свойство пропорции (если a:b=c:d, то ad = bc)

20 * 3 = MN * 5

5MN = 60

MN = 60 : 5

MN = 12 (см)

#SPJ1