Question

Помогите срочно даю 100балов Задание №436 с Г Д З мне не нужно там непонятно

Answer 1

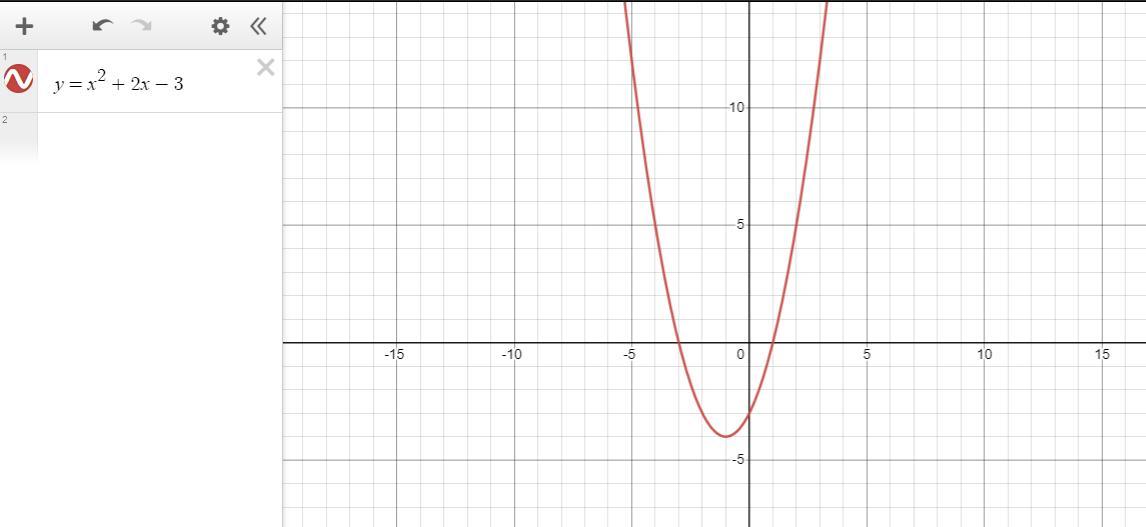
f(x)=x^2+2x-3

Снизу прикрепил график нашей функции для удобства нашего исследования функции.

1)

Чтобы найти значение функции надо подставить значение икса в нашу функцую

f(1)=1^2+2*1-3=0

f(-2.5)=(-2.5)^2+2*(-2.5)-3= -1.75

f(1.5)=(1.5)^2+2*(1.5)-3=2.25

f(1)=0, f(-2.5)= -1.75, f(1.5)=2.25

2)

Чтобы найти значение икса надо прировнять значение функции в нашу функцию

f(x) = 5 = x^2+2x-3 => $x_{1}$=2, $x_{2}$= -4

f(x) = -4 = x^2+2x-3 => x= -1

f(x) = -2 = x^2+2x-3 => $x_{1}$= $-1+\sqrt{2}$, $x_{2}$= $-1-\sqrt{2}$

f(2) = f(-4) = 5

f(-1) = -4

f($-1+\sqrt{2}$) = f($-1-\sqrt{2}$) = -2

3)

Чтобы найти точку пересечения с осью x, подставим 0 вместо y и решим уравнение относительно x.

Чтобы найти точку пересечения с осью y, подставим 0 вместо x и решим уравнение относительно y.

f(x)∩Ox: f(x)=0 => 0=x^2+2x-3 => (1,0),(−3,0)

f(x)∩Oy: f(0)  => y=0^2+2*0-3 => (0,-3)

4)

f(x)$\geq$0

x^2+2x-3$\geq$0

(x+3)(x-1)$\geq$0

x∈(-∞ ; -3 ]∪[ 1 ; +∞)

f(x)<0

x^2+2x-3<0

(x+ 3)(x-1)<0

x∈(3 ; -1)

f(x)$\geq$0, если x∈(-∞ ; -3 ]∪[ 1 ; +∞)

f(x)<0, если x∈( -3 ; 1 )

5)По-скольку наша функция имеет вид параболы с положительным знаком перед x^2, наша функция имеет только наименьшее значение. А значит наименьшее значение функции будет вершина параболы.

уравнение вершины параболы:

x= $-\frac{b}{2a}$ = $-\frac{2}{2} = -1$

а потом подставляем значение аргумента чтобы найти наименьшее значение функции

f(-1)=(-1)^2+2*(-1)-3=-4

Значит наименьшее значение функции у нас будет равно -4.

f(x)min= -4

А наибольшее значение функции не существует ведь ветви параболы смотрят вверх, то есть растет бесконечно.

6)

Область значение функции это значения которую может принимать аргумент функции, то есть наш икс. А по-скольку наша функция парабола, у нашего икса все значения допустимы.

D(y)∈R

7)

По-скольку наша функция парабола, её точка перегиба будет вершиной параболы. А ветви параболы смотрят вверх, значит она бесконечно убывает до точки перегиба и обратно бесконечно возрастает из точки перегиба.

У нас уже есть координаты вершины параболы: (-1;-4)

Следовательно,

если х∈(-∞ ; -1], то наша функция убывает

если х∈[-1 ; +∞), то наша функция возрастает

Надеюсь что все было понятно и на хорошую оценку ответа :)