Ответы
Ответ дал:
1
Критические точки: x1=0, x2=-2
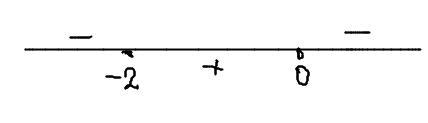
Найдем, какие из этих точек являются экстремумами и промежутки возрастания и убывания функции на числовой оси (см. рисунок 1):
По рисунку видно, что функция убывает до -2, затем возрастает до 0 и затем снова убывает. Следовательно
Промежутки убывания: (-∞;-2)∪(0;∞)
Промежуток возрастания: (-2;0)
Минимум: -2
Максимум: 0
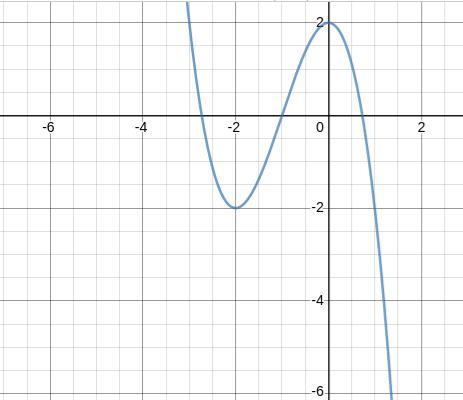
График см. рисунок 2
Приложения:
Аноним:
Обнови страницу, я немного изменил ответ.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад