Question

Срочно!! Помогите с 9.Даю 55 баллов.Если не сложно ещё и с 10 пожалуйста

Answer 1

Ответ:

9. Большее основание равно 22 см.

10. Периметр МКЕН равен 56 см.

Пошаговое объяснение:

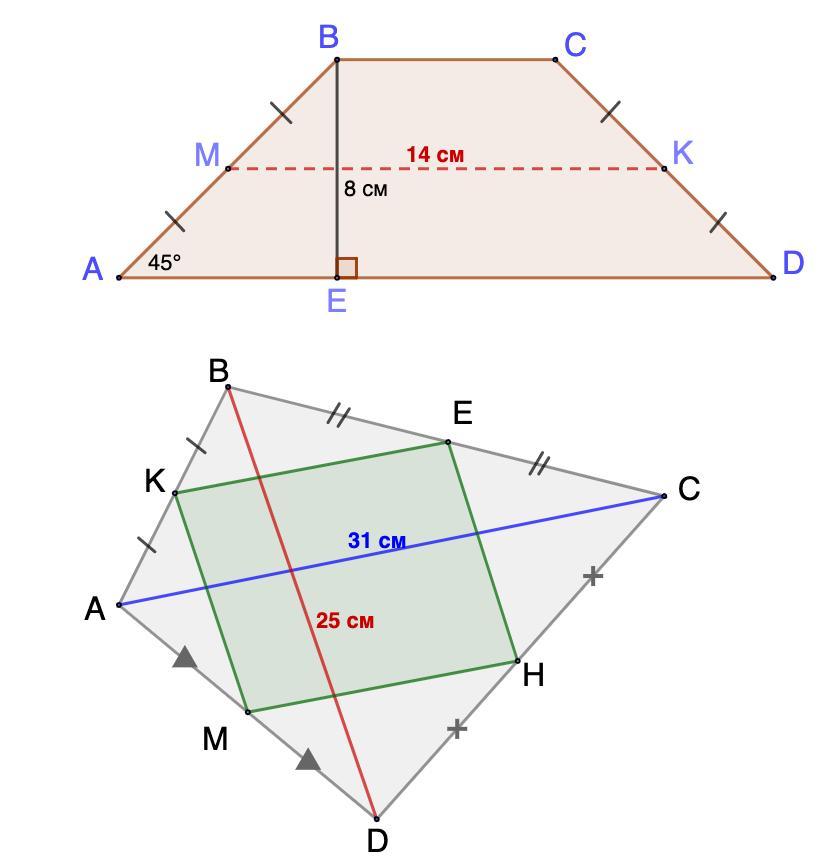
9. Один из углов равнобедренной трапеции равен 45°, высота 8 см, а средняя линия равна 14 см. Найти большее основание трапеции.

10. Диагонали четырехугольника равны 25 см и 31 см. Найти периметр четырехугольника, вершины которого являются серединами данного четырехугольника.

9. Дано: ABCD - равнобедренная трапеция;

∠А = 45°;

ВЕ = 8 см - высота; МК = 14 см - средняя линия.

Найти: AD

Решение:

Рассмотрим ΔАВЕ - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АВЕ = 90° - 45° = 45°

• Если в треугольнике два угла равны, то он равнобедренный.

⇒ АЕ = ВЕ = 8 см.

• Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание на части, большая из которых равна полусумме оснований.

• Средняя линия равна полусумме оснований трапеции.

⇒ ED = MK = 14 см.

AD = AE + ED = 8 + 14 = 22 (см)

Большее основание равно 22 см.

10. Дано: ABCD.

М, К, Е, Н - середины сторон AD, AB, BC, CD соответственно.

АС = 31 см; BD = 25 см.

Найти: Р(МКЕН)

Решение:

1. Рассмотрим ΔАВС.

АК = КВ; ВЕ = ЕС ⇒ КЕ - средняя линия.

• Средняя линия равна половине длины стороны, которую она не пересекает, и параллельна ей.

$\displaystyle KE=\frac{1}{2} AC = \frac{31}{2} =15,5$  (см)

2. Рассмотрим ΔАВD.

АM = MD; CH = HD ⇒ MH - средняя линия.

$\displaystyle MH=\frac{1}{2} AC = \frac{31}{2} =15,5$  (см)

3. Аналогично из ΔABD и ΔDBC ⇒ MK и ЕН - средние линии этих треугольников.

Тогда

$\displaystyle MK=EH =\frac{1}{2} BD = \frac{25}{2} =12,5$  (см)

4. Найдем периметр МКЕН.

• Периметр - сумма длин всех сторон.

Р(МКЕН) = КЕ + ЕН + МН + МК = 15,5 + 12,5 + 15,5 + 12,5 = 56 (см)

Периметр МКЕН равен 56 см.

* Полученная фигура МКЕН называется параллелограммом Вариньона.