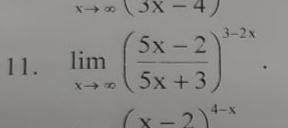Ответы
Ответ дал:
1
Ответ: e²
Пошаговое объяснение:
- 5/(5x+3)=1/t => 5x+3=-5t=> 5x=-5t-3 => x=-t-3/5
-2x=2t+6/5 3-2x = 2t+21/5
=> =
==
=
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад