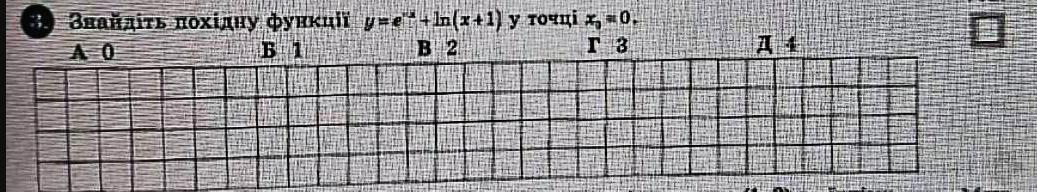Ответы
Ответ дал:
2
Ответ:
y'(0) = 0, ответ: А. 0
Объяснение:
Найти производную функции
в точке х₀ = 0
Понадобятся формулы производных сложной функции:
- Производная суммы равна сумме производных.
Найдем производную:
Теперь найдем значение производной в точке х₀ = 0:
Ответ: А. 0
#SPJ1
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад