Ответы
Ответ дал:
2
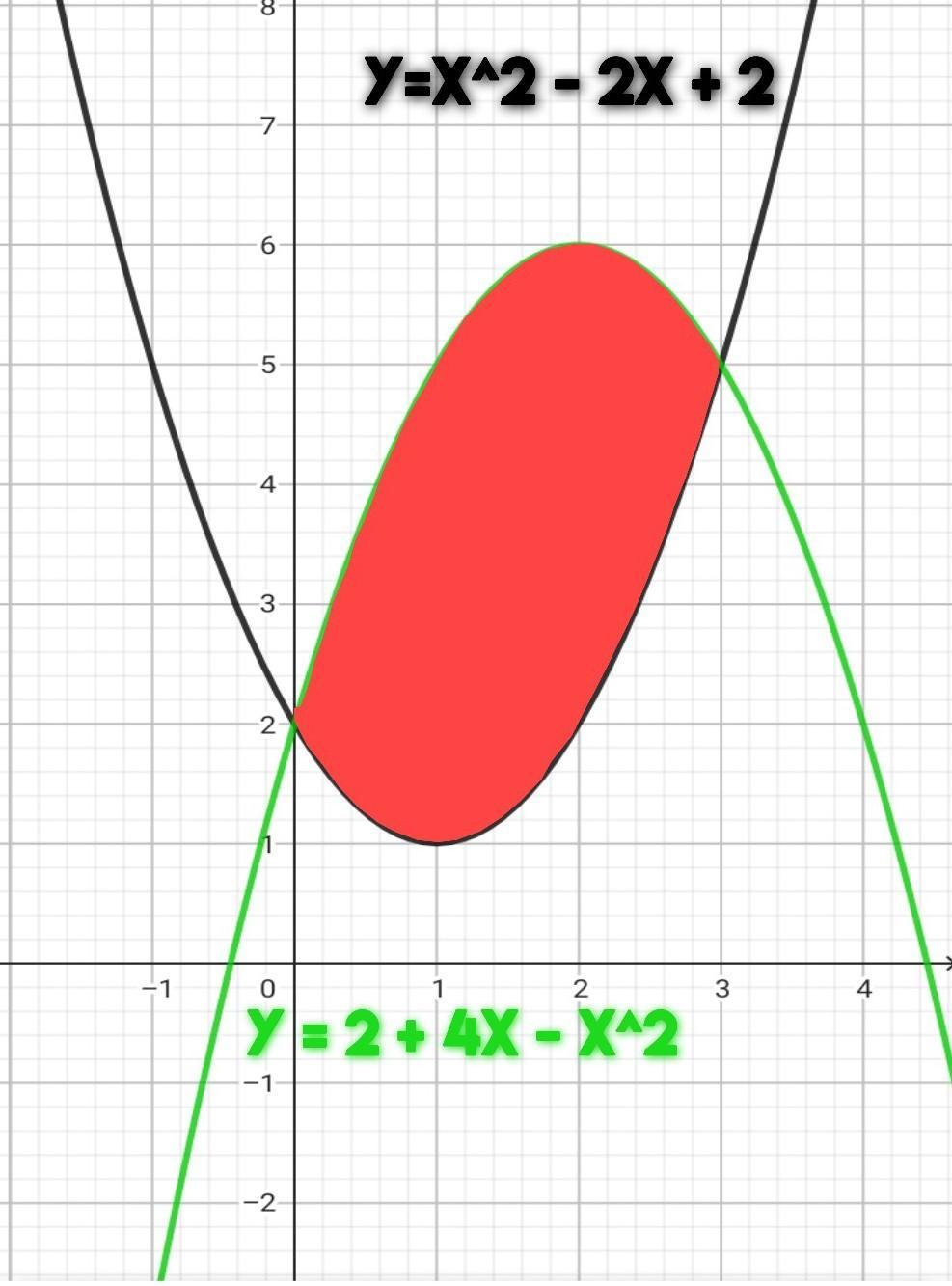
y = x² - 2 x + 2 – черная парабола, ветви вверх, вершина (1;1).
у = 2 + 4х - х² – зеленая парабола, ветви вниз, вершина (2;6).
Найдем точки пересечения:
2 + 4х - х² = х² - 2х + 2
4х - х² = х² - 2х
6х - 2х² = 0
х(6-2х) = 0
х = 0 или 6-2х = 0; -2х = -6 ⇒ х = 3
Площадь криволинейной трапеции найдем с помощью определенного интеграла, в пределах от 0 до 3, т.е. фигуру, с красным оттенком.
Ответ: S = 9eд²
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад
8 лет назад