Ответы
Ответ дал:
2
Ответ:
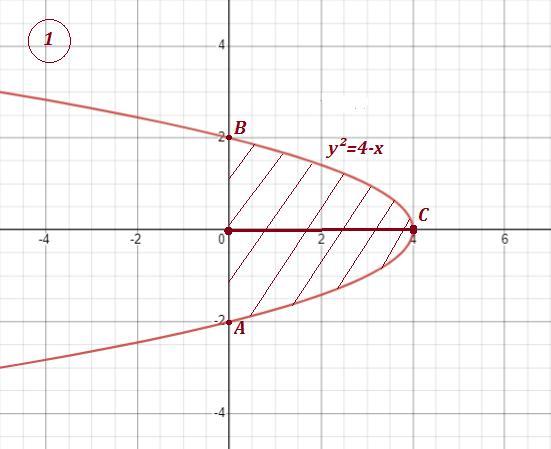
1) Объём тела вращения, образованного вращением криволинейной трапеции вокруг оси ОХ, равен .
Точки пересечения с ОУ:
Точки пересечения с ОХ: .
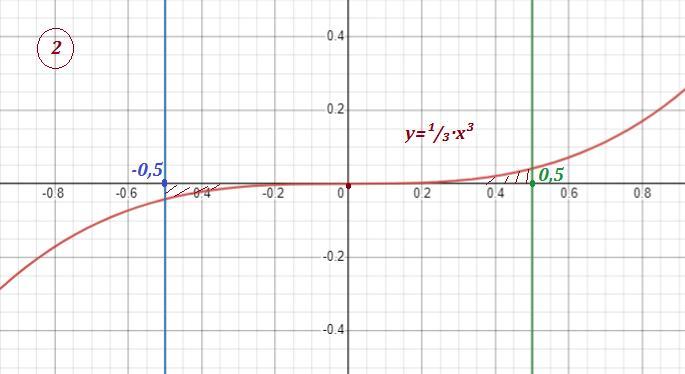
2) Площадь поверхности вращения рассчитывается по формуле:
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
