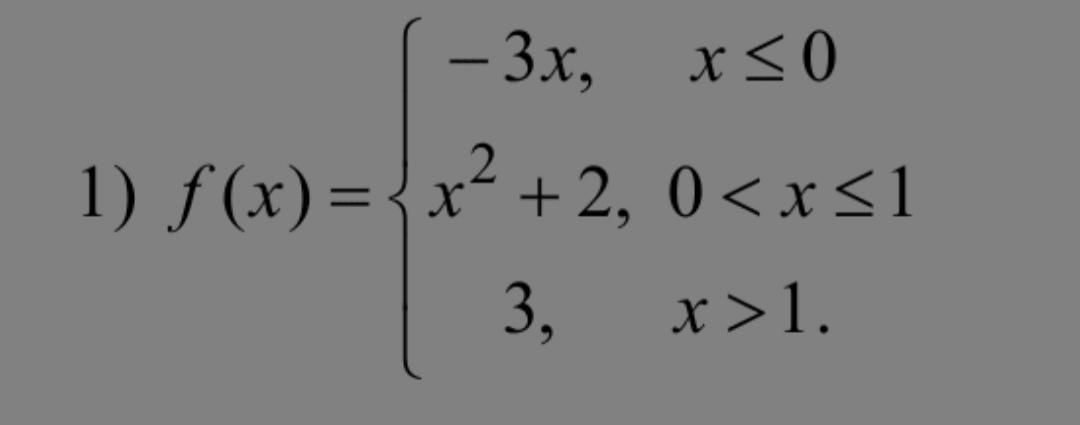Question

Дослідити на неперервність функцію.Побудувати її графік

Answer 1

Ответ:

Функция разрывна только в точке x = 0

Пошаговое объяснение:

Перевод: Исследовать на непрерывность функцию. Построить ее график.

$\displaystyle f(x)=\left \{\begin{array}{ccc}-3 \cdot x, \;\;\; x\leq 0\\x^2+2, \;\; 0 < x\leq 1\\3, \;\;\; x > 1\end{array}.$

Нужно знать: Если в точке x₀ функция f(x) определена и

1) выполняются все равенства f(x₀–0) = f(x₀), f(x₀) = f(x₀+0) и f(x₀–0) = f(x₀+0), то она непрерывна в точке x₀;

2) не выполняется один из равенств f(x₀–0) = f(x₀) или f(x₀) = f(x₀+0) или f(x₀–0) = f(x₀+0), то она разрывна в точке x₀.

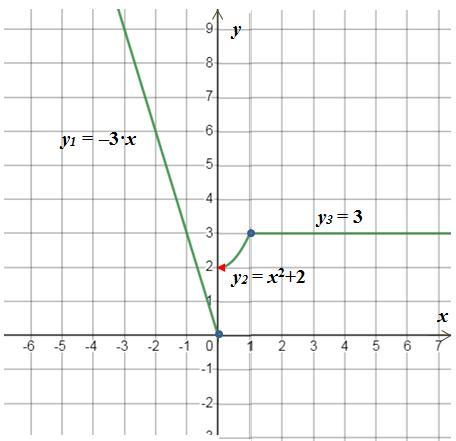
Решение. Каждая из функций y₁ = –3·x, y₂ = x²+2 и y₃ = 3 определена и непрерывна на R. Поэтому нам остаётся проверить на непрерывность в точках склеивания, то есть при x = 0 и x = 1.

1) x₀ = 0:

f(0) = –3·0 = 0, f(0–0) = –3·(0–0) = 0, f(0+0) = (0+0)²+2 = 2,

то есть f(0) = f(0–0) ≠ f(0+0) - функция разрывна;

2) x₀ = 1:

f(1) = 1²+2 = 3, f(1–0) = (1–0)²+2 = 3, f(1+0) = 3,

то есть f(0) = f(0–0) = f(0+0) - функция непрерывна.

График в приложенном рисунке.

#SPJ1