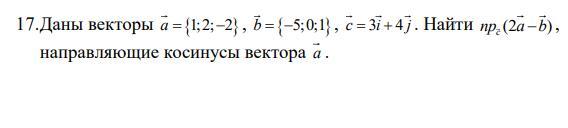Question

Помогите, пожалуйста! Задание на фото:

Answer 1

Ответ:

Даны векторы  

$\bf \vec{a}=\{1;2;-2\}\ ,\ \vec{b}=\{-5;0;1\}\ ,\ \vec{c}=3\vec{i}+4\vec{j}\ \ \to \ \ \vec{c}=\{3;4;0\}$

Найти проекцию вектора  $\bf 2\vec{a}-\vec{b}$  на вектор   $\bf \vec{c}$  :  пр.$\bf {}_{\vec{c}}\, (2\vec{a}-\vec{b})$  .

$\bf 2\vec{a}-\vec{b}=\{2+5\, ;4-0\ ;-4-1\}=\{7\, ;4\, ;-5\, \}$  

Скалярное произведение  $\bf (2\vec{a}-\vec{b})\cdot \vec{c}=7\cdot 3+4\cdot 4-5\cdot 0=21+16=37$

Длина вектора  $\bf |\, \vec{c}\, |=\sqrt{3^2+4^2+0^2}=\sqrt{25}=5$  

пр.$\bf {}_{\vec{c}}\, (2\vec{a}-\vec{b})=\frac{37}{5}=7,4$    

Направляющие косинусы вектора  $\bf \vec{a}$  равны  

$\bf cos\alpha =\dfrac{x_{a}}{|\vec{a}|}\ ,\ cos\beta =\dfrac{y_{a}}{|\vec{a}|}\ ,\ cos\gamma =\dfrac{z_{a}}{|\vec{a}|}$   .

$\bf |\, \vec{a}\, |=\sqrt{1^2+2^2+(-2)^2}=\sqrt{1+4+4}=\sqrt9=3\\\\cos\alpha =\dfrac{1}{3}\ ,\ cos\beta =\dfrac{2}{3}\ ,\ cos\gamma =-\dfrac{2}{3}$