Алгебра 11 клас.
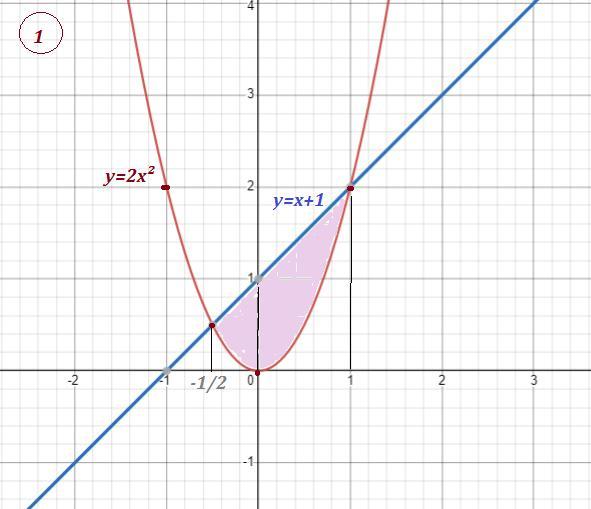
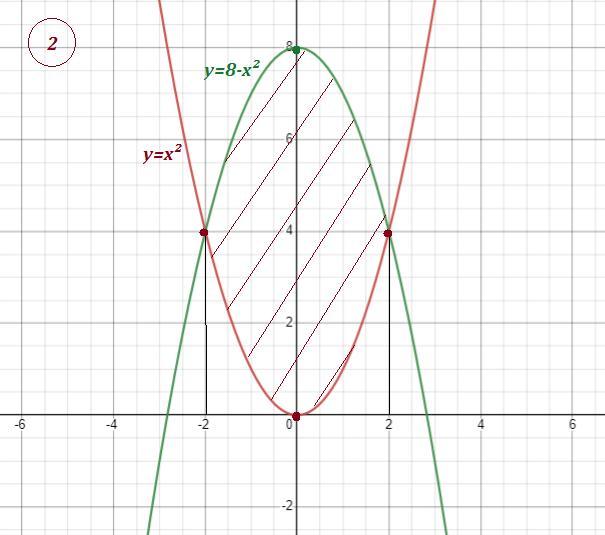
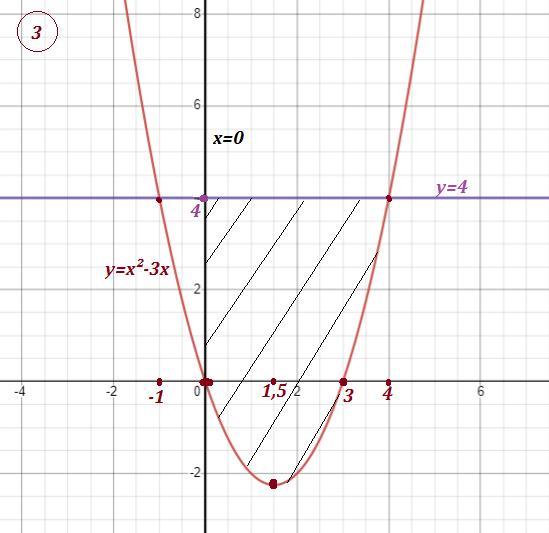
Знайти площу 4)у=2х² і у=х+1 5) у=х² і у=8-х² 6)у=х²-3х ;у=4 і х=0,за умови,що х більше або дорівнює 0.
Ответы
Ответ дал:
1
Ответ:
Вычисляем площадь области как разность площадей криволинейных трапеций .
Точки пересечения :
Точки пересечения:
Точки пересечения:
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
8 лет назад
8 лет назад