Question

помогите пожалуйста ​

Answer 1

Ответ:

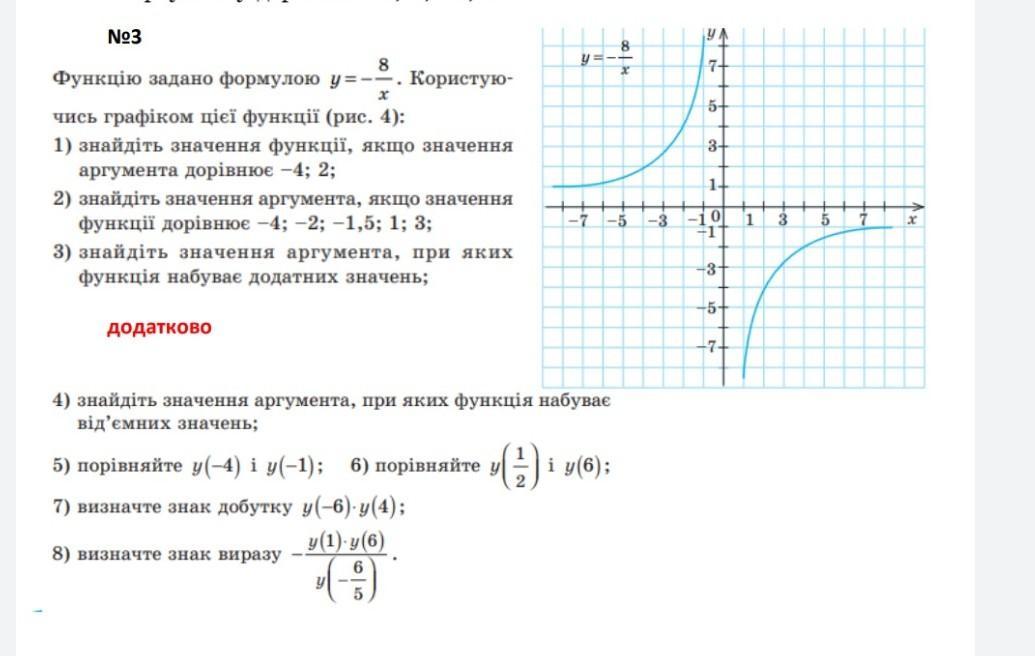
Функция задана формулой   $\bf y=-\dfrac{8}{x}$  .

$\bf 1)\ \ y(-4)=-\dfrac{8}{-4}=2\ \ ,\ \ \ \ y(2)=-\dfrac{8}{2}=-4$  

$\bf 2)\ \ y=-4\ \ \Rightarrow \ \ \ -4=-\dfrac{8}{x}\ \ ,\ \ x=-\dfrac{8}{-4}=2\\\\\\y=-4\2\ \ \Rightarrow \ \ \ -2=-\dfrac{8}{x}\ \ ,\ \ x=-\dfrac{8}{-2}=4\\\\\\y=-1,5\ \ \Rightarrow \ \ \ -1,5=-\dfrac{8}{x}\ \ ,\ \ x=-\dfrac{8}{-1,5}=5\dfrac{1}{3}\\\\\\y=1\ \ \Rightarrow \ \ \ 1=-\dfrac{8}{x}\ \ ,\ \ x=-\dfrac{8}{1}=-8\\\\\\y=3\ \ \Rightarrow \ \ \ 3=-\dfrac{8}{x}\ \ ,\ \ x=-\dfrac{8}{3}=-2\dfrac{2}{3}$  

3)  Функция принимает положительные значения, то есть   $\bf y > 0$  , график находится выше оси ОХ ,  когда   $\bf x\in (-\infty \, ;\ 0\ )$  .

4)  Функция принимает отрицательные значения, то есть   $\bf y < 0$  , график находится ниже оси ОХ , когда   $\bf x\in (\ 0\ ;+\infty \, )$  .

$\bf 5)\ \ y(-4) < y(-1)\\\\6)\ \ y\Big(\dfrac{1}{2}\Big) < y(6)\\\\7)\ \ \underbrace{\bf y(-6)}_{ > 0}\cdot \underbrace{\bf y(4)}_{ < 0} < 0$

8)  Так как по графику можно определить, что  $\bf y(1) < 0\ ,\ y(6) < 0$  , то  

произведение  $\bf y(1)\cdot y(6) > 0$ . Также определяем, что  $\bf y\Big(-\dfrac{6}{5}\Big) > 0$  .

Поэтому

                  $\bf -\dfrac{y(1)\cdot y(6)}{y\Big(-\dfrac{6}{5}\Big)} < 0$  .

Answer 2

Відповідь:

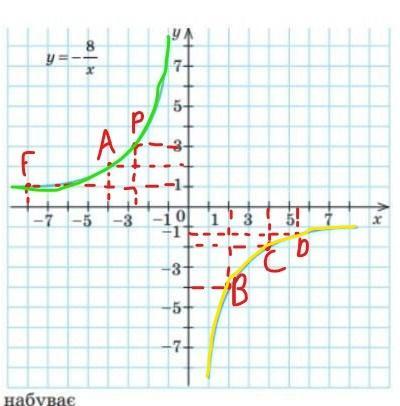
1) коли x = -4, y = 2, на рисунку точка А

коли x = 2, y = -4, на рисунку точка B

2) y = -4, x = 2, точка В

y = -2, x = 4, точка С

y = -1,5, x = 5,3, точка D

y = 1, x = -8, точка F

y = 3, x = -2,6, точка P

3) функція набуває додатніх значень при усіх від'ємних значеннях аргумента (виділена зеленим кольором)

4) функція набуває від'ємних значень при усіх додатніх значень аргумента (виділена жовтим кольором)

5) 2 < 8

6) -16 < -1,2

7) додатнє*від'ємне = від'ємне

8)-(-*-)/+ = -/+ = -

Пояснення: