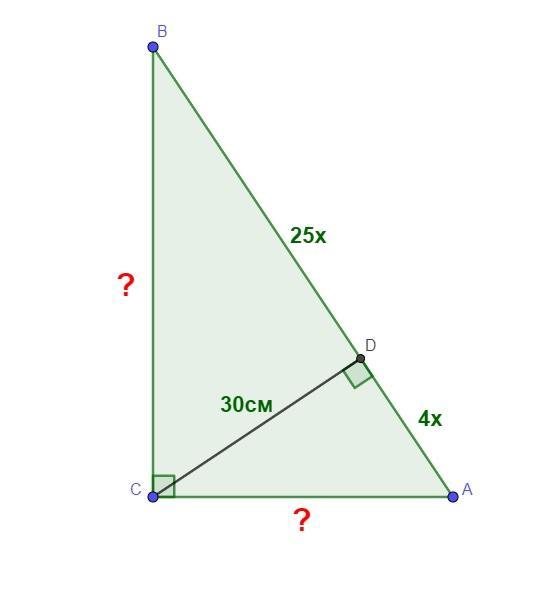
Висота прямокутного трикутника дорівнює 30см, проведена до
гіпотенузи, ділить її на відрізки у відношенні 4:25. Знайти катети
трикутника. ПОМОГИТЕ СРОЧНО ДАЮ 50 БАЛЛОВ
Ответы
Ответ:
Катети прямокутного трикутника дорівнюють 6√29 (см) і 15√29 (см)
Объяснение:
Висота прямокутного трикутника дорівнює 30см, проведена до гіпотенузи, ділить її на відрізки у відношенні 4:25. Знайти катети.
Метричні співвідношення в прямокутному трикутнику:
- Квадрат висоти прямокутного трикутника, проведеної до гіпотенузи, дорівнює добутку проекцій катетов на гіпотенузу.
(1) CD²=AD·DB
- Квадрат катета дорівнює добутку гіпотенузи і проєкції цього катета на гіпотенузу.
(2) AC²=AB·AD
(3) CB²=AB·DB
Дано: ΔАВС(∠С=90°), СD⊥AB, CD=30 см, AD:DB=4:25
Знайти: АС, СB
Розв'язання:
1.
Нехай AD=4x, DB=25x, де x - коефіцієнт пропорційності між сторонами AD і DB. Тоді за метричним співвідношенням (1) у прямокутному трикутнику маємо:
CD²=AD·DB
30²=4х·25х
100х²=900
х²=9
х=3
AD=4x=4·3= 12 (см), DB=25x=25·3= 75 (см)
Гіпотенузу знаходимо через суму відрізків:
АВ=AD+DB=12+75= 87 (см)
2.
За метричним співвідношенням (2) у прямокутному трикутнику маємо:
AC²=AB·AD
AC²=87·12=1044
(см)
3.
За метричним співвідношенням (3) у прямокутному трикутнику маємо:
CB²=AB·DB
CB²=87·75=6525
(см)
Відповідь: АС=6√29 (см), СВ=15√29 (см)
#SPJ1