2. В прямоугольном треугольнике гипотенуза равна 20 см, один его катет на 4 см больше другого. Чему равны катеты этого треугольника? (Используя теорему Пифагора)
Ответы
Ответ дал:
1
Ответ:
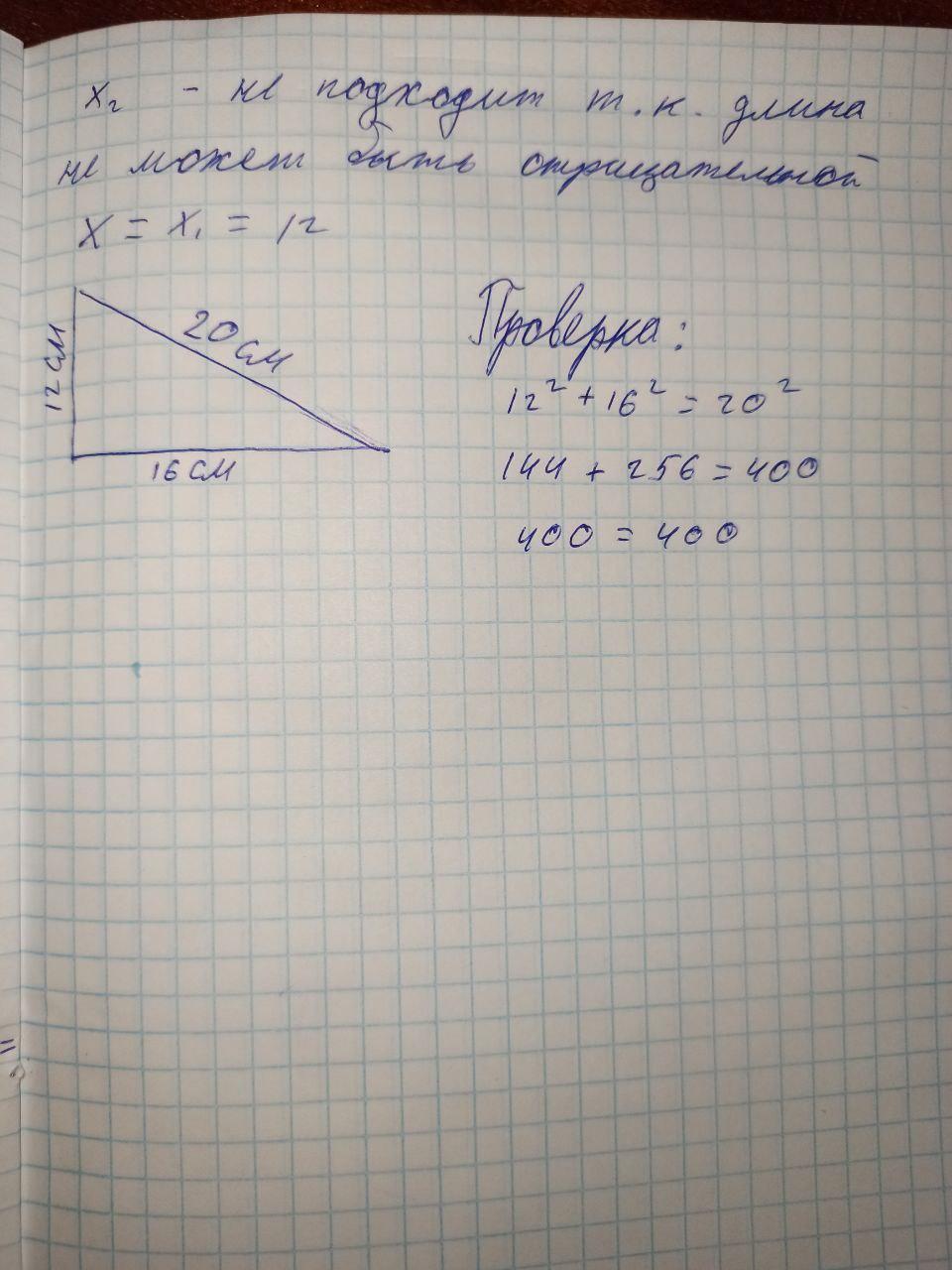
х = 12
Объяснение:
Надеюсь поччерк поймёте)
Приложения:
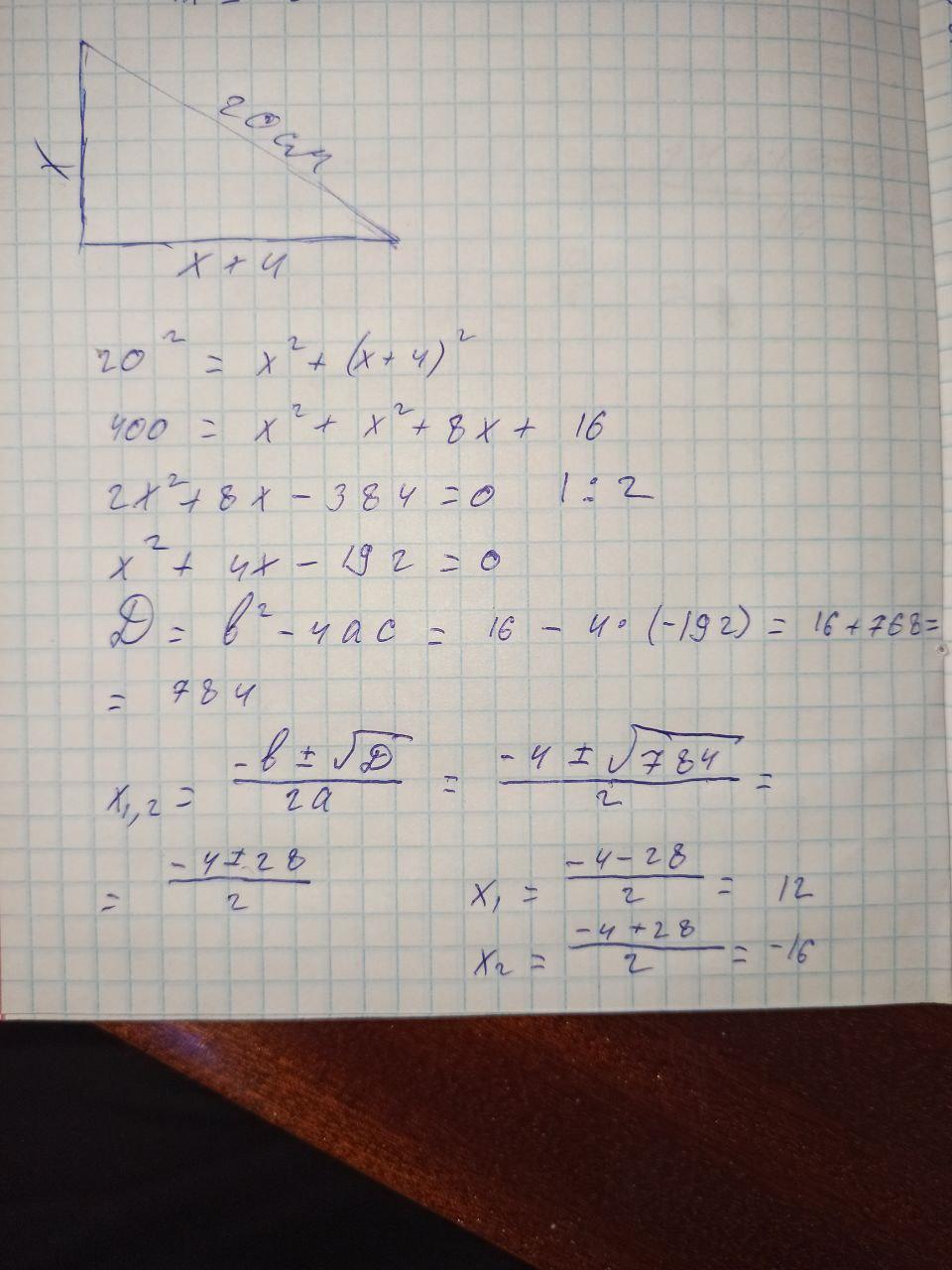
Ответ дал:
1
Ответ: МОЖНО КОРОНУ, ПОЖАЛУЙСТА
Объяснение:
треугольник АВС
ВС гипотенуза=20см
АВ=?
АС=?, на 4 см больше чем АВ
Пусть сторона АВ=х см, тогда сторона АС=х+4 см. За теоремой Пифагора ВС²=АВ²+АС²
20²=х²+(х+4)²
20х²-х²-(х+4)²=0
400-х²-х²-8х-16=0
384-2х²-8х=0
-2х²-х+384=0
D=(-8)²-4(-2)×384=3136
корень с D=56
x1=-(-8)-56/2×(-2)=-48/-4=12(см) катет АВ
х2=-(-8)+56/2×(-2)=64/-4=-16(см) не подходит тк меньше нуля, а катет не может быть меньше нуля
АС=АВ+4=12+4=16(см)
Ответ: катет АВ=12 см; АС=16см
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад