Предмет: Геометрия
Автор: KORT11
Вопрос задан 1 год назад

ЗАДАЧА НА РИСУНКЕ.
СРОЧНО НАДО РЕШИТЬ

Приложения:

Ответы

Ответ дал: emil4ikono

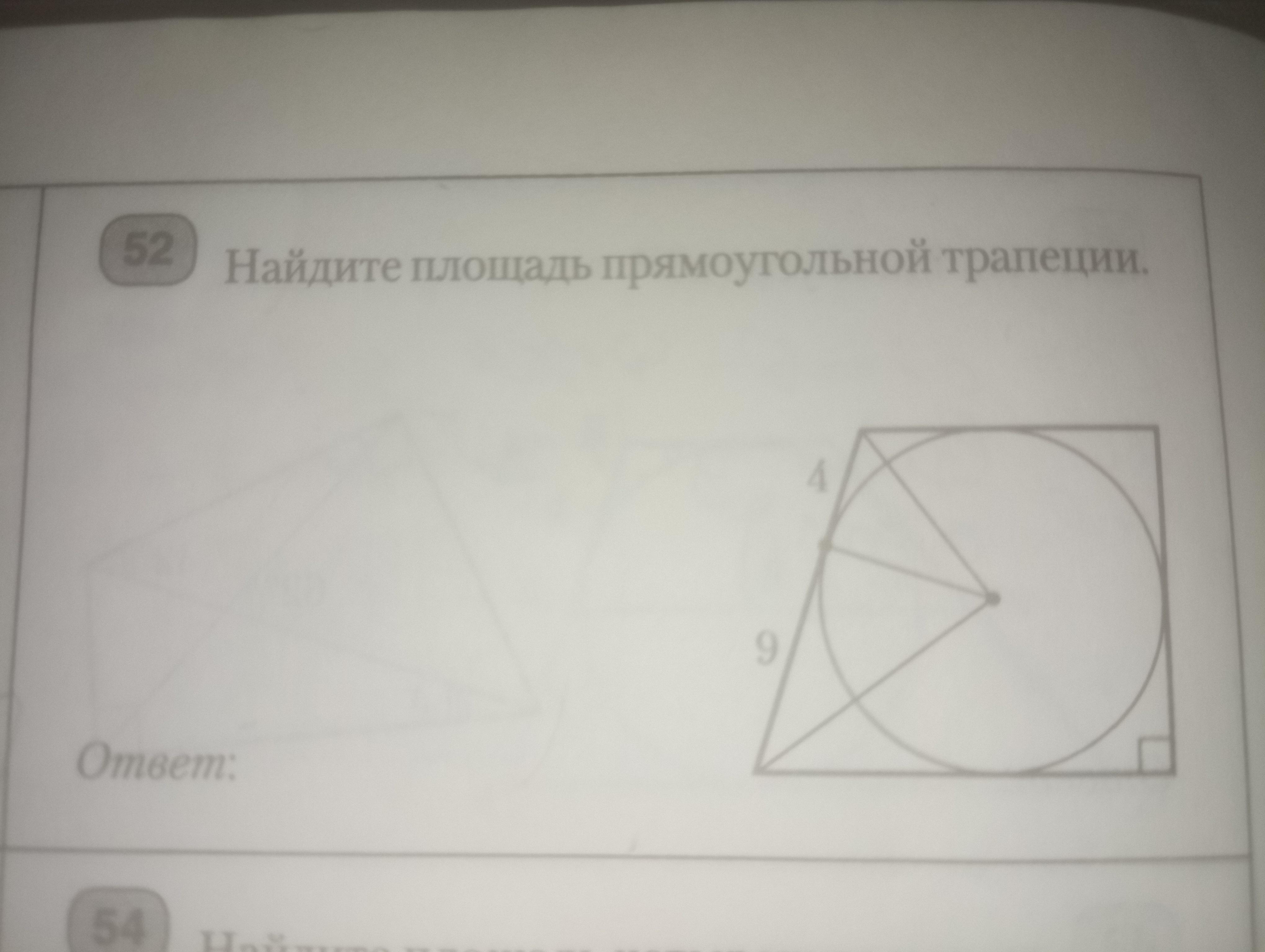
Если в четырехугольник можео вписать окружность, то суммы противоположных сторон равны. Полупериметр: р =12+9 = 21 Площадь: S = rp = 5 * 21 = 105

KORT11: Это не то

emil4ikono: В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Если в четырехугольнике есть AB+CD=AD+BC, то в него можно вписать окружность. => Периметр равен: P = 2 * (12+9) = 42 p = P\2 = 42\2 = 21 S = V(p-a)(p-b)(p-c)(p-d) Так как a = c и b=d, то: S = V[(p-a)^2 * (p-b)^2] = (p-a)(p-b) = (21-12)(21-9) = 9*12 = 108

emil4ikono: Так?

Вас заинтересует

Другие предметы

1 год назад

Сколько всего новых слов можно получить из слова «Прыжок» путём перестановки букв в нём?

Математика

1 год назад

57. Найдите значение выражения 3,3-1,(6) - A) 5 C) 3 B) 239 50 D) -|~ 77 20 E) 4 Е)4

Математика

1 год назад

Помогите пожалуйста решить

Українська мова