Складіть рівняння прямої, яка проходить через точки:
Вирішити третє і четверте, те ще обчедене. Необхідно, щоб було пояснення, яка сама пряма з букв є вона вертикальною, невертикальною, горизонтальною, чи ще якою і чому, математично пояснити чому саме така пряма. Оскільки це ..... пряма, то її рівняння ....... Повне вирішення рівняння, покрокове пояснення тд.
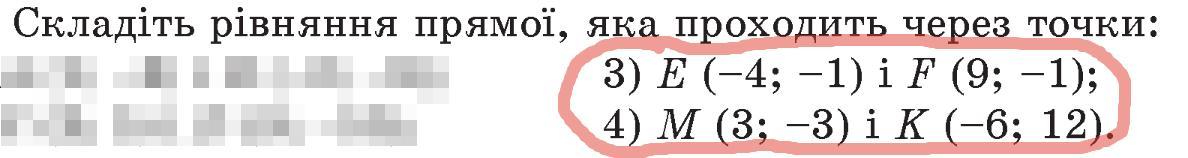
Ответы
Ответ:
3) Прямые, перпендикулярные оси ОХ ( вертикальные, параллельные оси ОУ) ,имеют уравнения вида х=а , где а - некоторое число , Точки на этой прямой имеют одинаковые абсциссы (первые координаты), равные а , а ординаты (вторые координаты) - произвольные числа .
Прямые, перпендикулярные оси ОУ ( горизонтальные, параллельные оси ОХ) , имеют уравнения вида у=а , где а - некоторое число. Точки на этой прямой имеет одинаковые ординаты, равные а , а абсциссы - произвольные числа .
Можно заметить, что у точек Е (-4 ; -1 ) и F( 9 ; -1) ординаты одинаковы и равны -1 . Поэтому прямая, проходящая через точки E
и F , будет иметь уравнение у = -1 .
4) Уравнение прямой имеет вид y = kx + b .
Чтобы составить уравнение прямой, проходящей через две точки,
M(3;-3) и K(-6;12) , можно подставить координаты этих точек в
уравнение y=kx+b. Тогда получим два верных равенства, из которых
найдём коэффициент k и свободный член b .
Вычтем из 1-го уравнения 2-ое, получим
Уравнение прямой МК имеет вид или
.
Угловой коэффициент прямой , поэтому угол наклона
этой прямой к положительному направлению оси ОХ, тупой.
Так как , то точка пересечения прямой МК с осью ОУ имеет координаты ( 0 ; 2 ) .
Замечание. Если бы мы решали 3 пример так же, как и 4-ый, то получили бы то же самое уравнение. Только решение было бы более объёмным и долгим .
По уравнению :
В котором :
На ноль делить нельзя , но можно воспользоваться свойством пропорции :
Это прямая параллельная оси абсцисс .
Это прямая наклонённая к оси абсцисс под тупым углом ,
так как k < 0 .