Точка О-середина оси цилиндра. Диаметр основания цилиндра виден из точки О под прямым углом, а расстояние от точки О до точки окружности основания цилиндра равно 2 см. Вычислите объем цилиндра.
Ответы
Ответ дал:
0
Точка О-середина оси цилиндра. Диаметр основания цилиндра виден из точки О под прямым углом, а расстояние от точки О до точки окружности основания цилиндра равно 2 см. Вычислите объем цилиндра.
Объем цилиндра равен произведению площади его основания на высоту.
V=SH
Все нужные измерения найдем с помощью т. Пифагора.
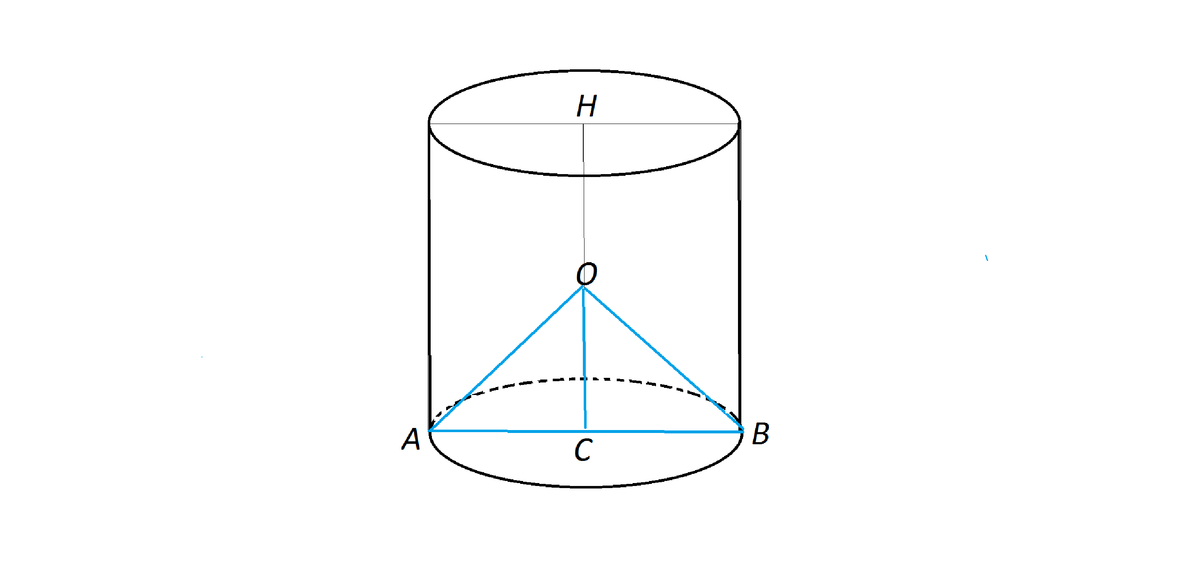
Точка О - вершина прямого угла равнобедренного прямоугольного треугольника АОВ
с катетами АО=ОВ=2 см
АВ - гипотенуза этого треугольника=диаметру основания и по т.Пифагора равна 2√2, следовательно,
радиус основания цилиндра (2√2):2=√2
СО- половина высоты цилиндра СН и равна радиусу основания, т.к.
ОС - медиана треугольника АОВ и по свойству прямоугольного треугольника равна половине АВ, =>
СО= АС=√2.
Высота цилиндра
СН =СО*2=2√2
V=SH=π(√2)²*2√2=4π√2 см³
Объем цилиндра равен произведению площади его основания на высоту.
V=SH
Все нужные измерения найдем с помощью т. Пифагора.
Точка О - вершина прямого угла равнобедренного прямоугольного треугольника АОВ
с катетами АО=ОВ=2 см
АВ - гипотенуза этого треугольника=диаметру основания и по т.Пифагора равна 2√2, следовательно,
радиус основания цилиндра (2√2):2=√2
СО- половина высоты цилиндра СН и равна радиусу основания, т.к.
ОС - медиана треугольника АОВ и по свойству прямоугольного треугольника равна половине АВ, =>
СО= АС=√2.
Высота цилиндра
СН =СО*2=2√2
V=SH=π(√2)²*2√2=4π√2 см³
Приложения:
Ответ дал:
0
а с чего взяли что точка О вершина прямого угла? Там может быть и не прямой угол. Сказано лишь то что диаметр к ней перпендикулярен, что в принципе и так следует из того что она лежит на оси цилиндра. Мне кажется задача составлена не корректно и с нехваткой данных.
Ответ дал:
0
а может вы и правы))))
Ответ дал:
0
Всё правильно. Диаметр основания цилиндра виден из точки О под прямым углом - вряд ли можно это понять как-то иначе, чем так: О - вершина прямого угла.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад