Question

У ΔABD CD — його бісектриса. AD=25 см , ВD=30 см і CB=18см. Знайти периметр ΔABD.​

Answer 1

Ответ:

Периметр △ABD дорівнює 88 см

Объяснение:

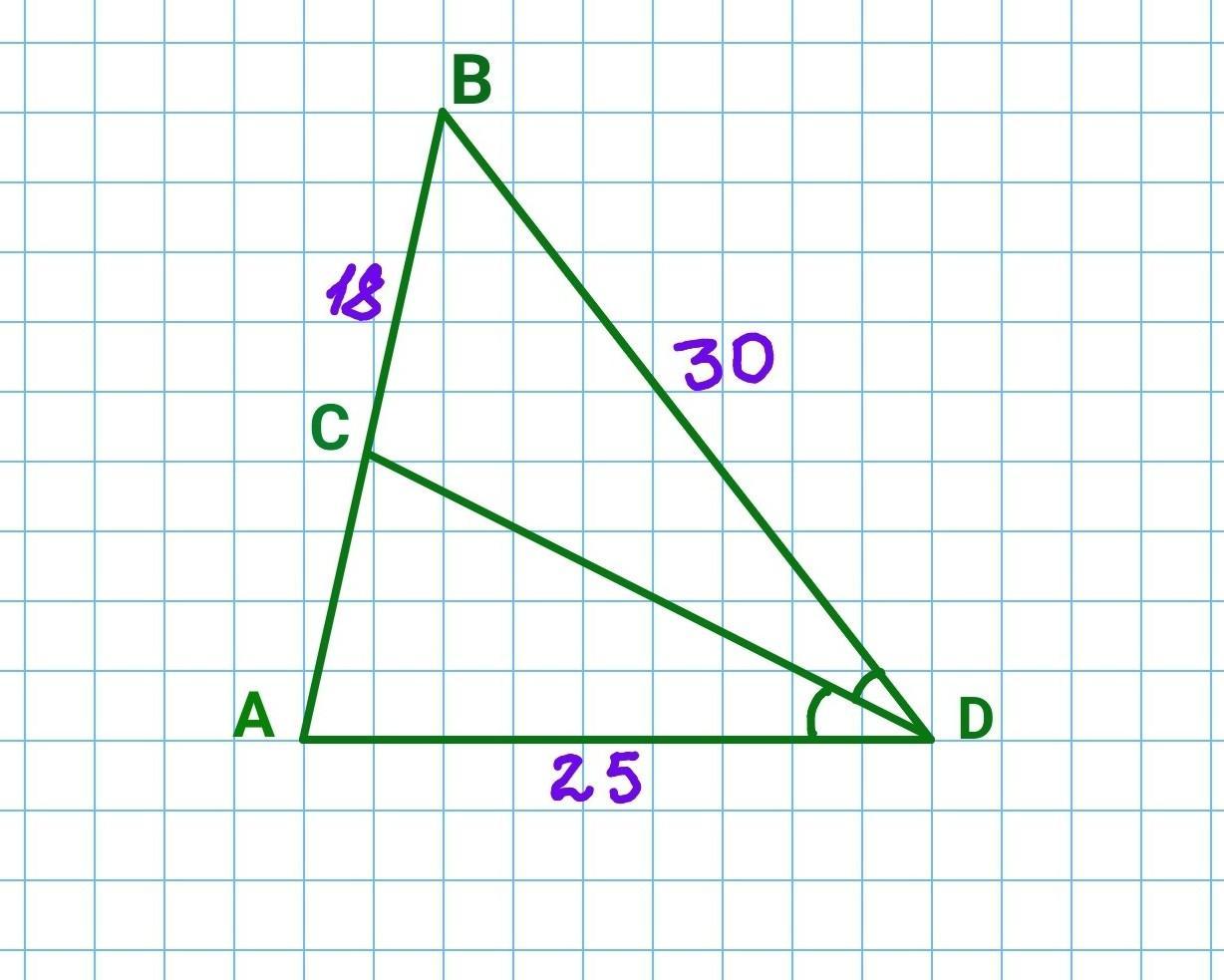
У ΔABD CD — його бісектриса. AD=25 см , ВD=30 см і CB=18см. Знайти периметр ΔABD.

• Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам. (властивість бісектриси).

За властивістю бісектриси маємо:

$\bf \dfrac{AD}{BD} = \dfrac{AC}{CB}$

Тоді:

$AC = \dfrac{AD\cdot CB}{BD} = \dfrac{25\cdot 18}{30} = \bf 15$ (см)

За аксиомою вимірювання відрізків отримаємо:

AB =AC+CB=15+18= 33 (см)

• Периметром трикутника називають суму довжин усіх сторін трикутника.

$\bf P_{ABD} = AB+BD + AD$

$\sf P_{ABD} = 33 + 30 + 25 =\bf 88$ (см)

Відповідь: 88 см

#SPJ1