Question

Найти стороны паралелограмма, если одна сторона меньше второй на 2 а диагонали равны 6 и 2 см

Answer 1

Объяснение:

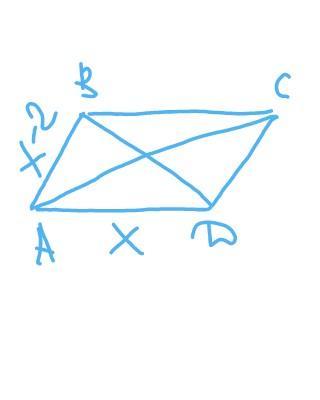
ABCD - параллеллограмм

сторона АD=BC=х см

сторона AB=CD=x-2 см

диагональ AC=6 см

диагональ BD=2 см

найти: АD;BC ; AB; CD

∆АВD:

по теореме косинусов:

ВD²=AB²+AD²-2•AB•AD•cos∠BAD

∆ABC:

AC²=AB²+BC²-2•AB•BC•cos∠ABC=

=AB²+BC²-2AB•BC•cos(180-∠BAD)

система:

{ВD²=AB²+AD²-2•AB•AD•cos∠BAD

{AC²=AB²+BC²-2•AB•AD•(-cos∠BAD)

{2²=(x-2)²+x²-2x•(x-2)•cos∠BAD

{6²=(x-2)²+x²+2x•(x-2)•cos∠BAD

{4=x²-4x+4+x²-(2x²-4x)•cos∠BAD

{36=x²-4x+4+x²+(2x²-4x)•cos∠BAD

{4-x²+4x-4-x²= -(2x²-4x)•cos∠BAD

{36-x²+4x-4-x²=(2x²-4x)•cos∠BAD

{-2x²+4x= -(2x-4x)•cos∠BAD

{32-2x²+4x=(2x-4x)•cos∠BAD

{2x²-4x=(2x-4x)•cos∠BAD

{32-2x²+4x=(2x-4x)•cos∠BAD

2x²-4x=32-2x²+4x

2x²-4x-32+2x²-4x=0

4x²-8x-32=0

x²-2x-8=0

D=(-2)²-4•1•(-8)=4+32=36

x1=(2-6)/2= -2 не подходит

х2=(2+6)/2=4 см

АD=ВС=4 см

АВ=СD=4-2=2 cм

ответ: АВ=2 см ; ВС=4 см; СD=2 cм; АD=4 cм