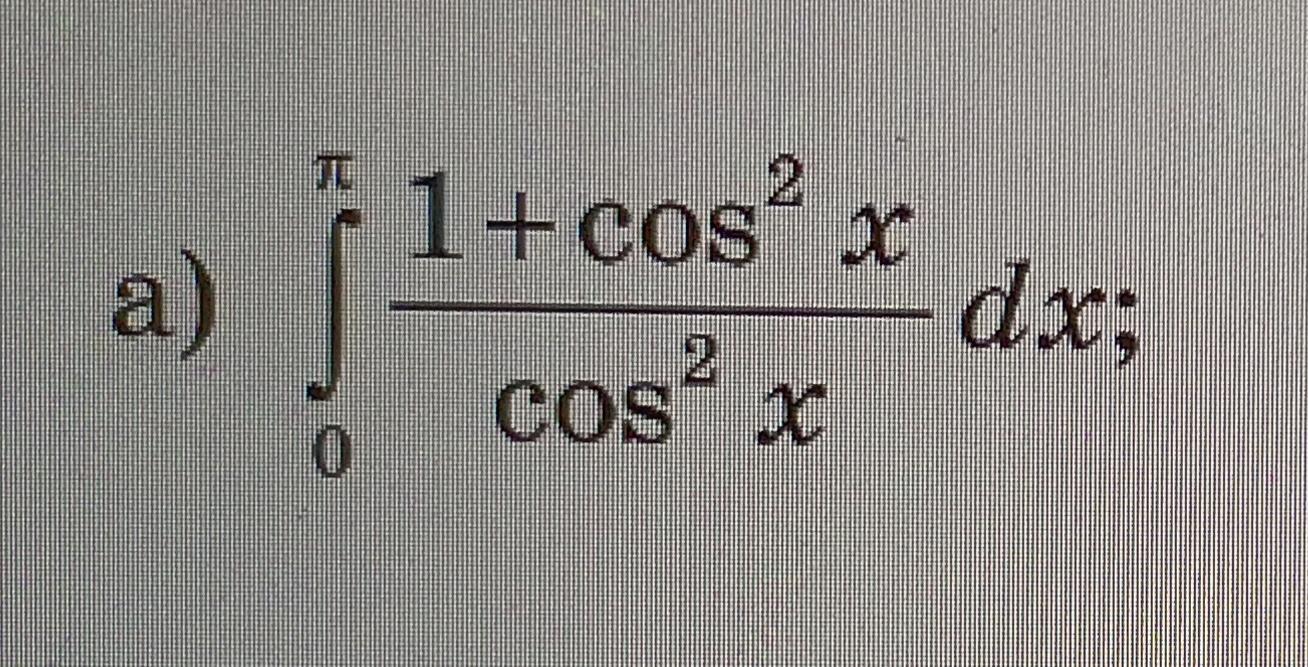Ответы
Ответ дал:
1
Ответ:
Объяснение:
Вычислить интеграл:
Это табличные интегралы:
Формула Ньютона - Лейбница:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад