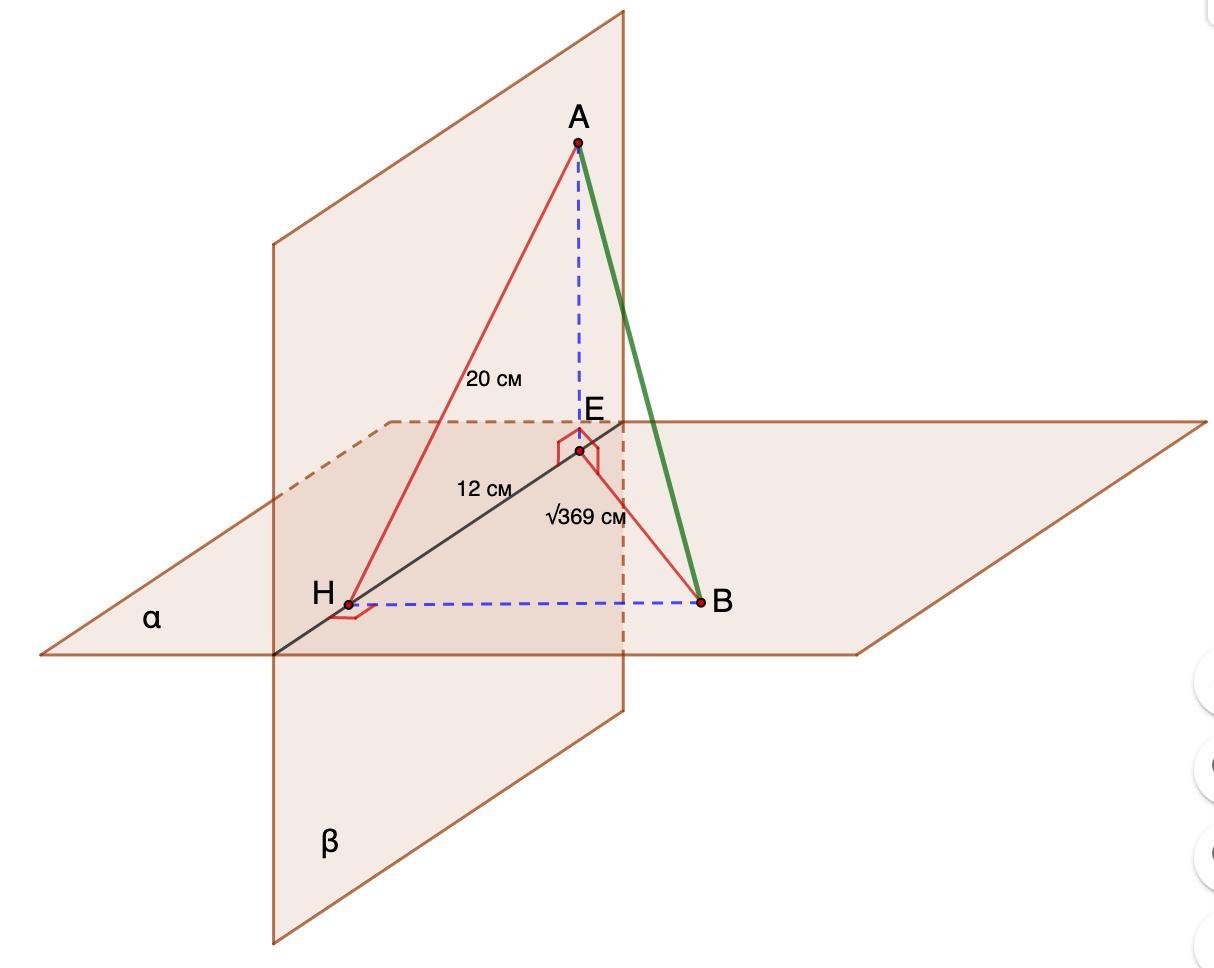
Кінці відрізка лежать у двох взаємно перпендикулярних площинах. Проекції відрізка на кожну із площин дорівнюють √369см і 20см відповідно. Відстань між основами перпендикулярів, проведених із кінців відрізка до площини, дорівнює 12см. Знайдіть довжину даного відрізка
Ответы
Ответ:
Длина данного отрезка равна 25 см.
Объяснение:
Концы отрезка лежат в двух взаимно перпендикулярных плоскостях. Проекции отрезка на каждую из плоскостей равны √369 см и 20 см соответственно. Расстояние между основаниями перпендикуляров, проведенных с концов отрезка к плоскости, равно 12 см. Найдите длину данного отрезка.
Дано: α ⊥ β.
А ∈ β; В ∈ α;
ЕВ = √369 см; НА = 20 см;
НЕ = 12 см.
Найти: АВ.
Решение:
- Проекцией наклонной на плоскость, называется отрезок, соединяющий основание перпендикуляра и основание наклонной.
⇒ ЕВ - проекция АВ на плоскость α; НА - проекция АВ на плоскость β.
- Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.
⇒ АЕ ⊥НЕ; АЕ ⊥ЕВ.
1. Рассмотрим ΔНАЕ - прямоугольный.
НА = 20 см; НЕ = 12 см.
По теореме Пифагора найдем АЕ:
АЕ² = НА² - НЕ² = 400 - 144 = 256 ⇒ АЕ = √256 = 16 (см)
2. Рассмотрим ΔЕАВ - прямоугольный.
ЕА = 16 см; ЕВ = √369 см.
По теореме Пифагора найдем АВ:
АВ² = ЕА² + ЕВ² = 256 + 369 = 625 ⇒ АВ = √625 = 25 (см)
Длина данного отрезка равна 25 см.
#SPJ1