прямоугольник ABCD расположен внутри сферы так, что его вершины лежат на поверхности сферы. Вычислите расстояние от центра сферы до плоскости ABC, если длины сторон прямоугольника равны 12 см и 16 см, а длина радиуса равна 11 см.
Ответы
Ответ дал:
0
Сделав рисунок, увидим, что прямоугольник АВСД принадлежит плоскости сечения сферы и вписан в окружность, ограничивающую это сечение,
и все его вершины лежат на этой окружности.
Расстояние от центра сферы до плоскости АВС - это расстояние от центра сферы до центра окружности, на которой расположены вершины АВСД.
Решение сводится к теореме Пифагора.
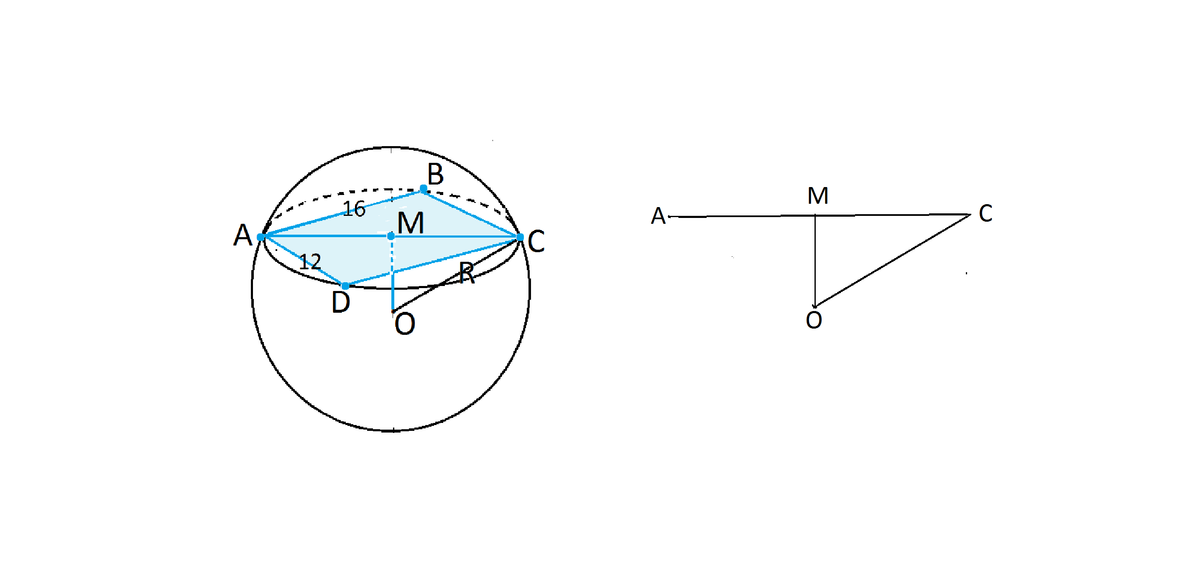
На рисунке, данном во вложении, МО - искомое расстояние и является катетом прямоугольного треугольника ОМС.
Второй катет МС - половина диагонали АВСД.
Эта половина - радиус сечения.
АМ - половина диагонали АС.
По т. Пифагора АС²=АВ²+ВС²=400
АС=√400=20 =>
МС=10
МО²=ОС²-МС²=121-100=21
МО=√21
и все его вершины лежат на этой окружности.
Расстояние от центра сферы до плоскости АВС - это расстояние от центра сферы до центра окружности, на которой расположены вершины АВСД.
Решение сводится к теореме Пифагора.
На рисунке, данном во вложении, МО - искомое расстояние и является катетом прямоугольного треугольника ОМС.
Второй катет МС - половина диагонали АВСД.
Эта половина - радиус сечения.
АМ - половина диагонали АС.
По т. Пифагора АС²=АВ²+ВС²=400
АС=√400=20 =>
МС=10
МО²=ОС²-МС²=121-100=21
МО=√21
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
11 лет назад