Срочно даю 40 баллов
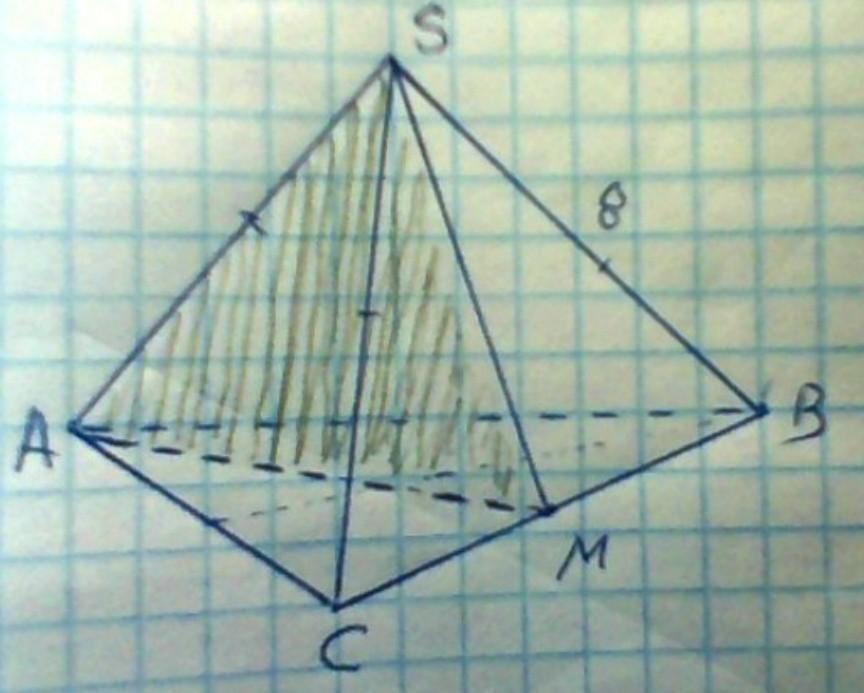
Постройте сечение пирамиды SABC плоскостью, проходящей через точку М-середину ребра AB и параллельной плоскости SAC. Найдите периметр полученного сечения,если каждое ребро пирамиды имеет длину 4.С чертежом и решением.
Помогите пожалуйста,срочно надо даю 40 балла. Зарание спасибо.
Ответы
Ответ дал:
0
походу так,
найдём площадь ∆ASM. вся грани этой пирамиды равны. поэтому AM=SM.
SM²=BS²=64-16=48
Добавим на рисунке отрезок MK/AS, точка К- середина АS ∆SKM:KM²=MS²-KS²=48-16=32.KM=√32=4√2.
Найдём площадь сечения ∆ASM S∆=0,5•8•4√2=16√2см²
наверно так
Приложения:
vjv26382:
спасибо огромное но нам сказали что ответ 6, поэтому к сожелению не правильно
(╥﹏╥)
спасибо огромное
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад