Question

Допожіт Будь ласка ТЕРМІНОВО. З точки до прямої проведено двi рiвнi сiж собою похилі. Проєкція однієї з них дорівнює 11 см. Знайдіть відстань між основами похилих.​

Answer 1

Ответ:

Объяснение:

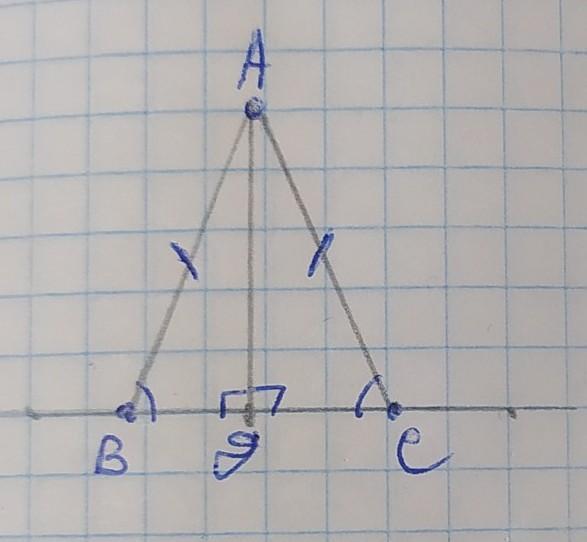
проекция ВД наклонной АВ=6см

проекция СД наклонной АС=6см

Объяснение:

Обозначим точку, из которой проведены наклонные - А, а точки и пересечения их с прямой В и С. В данном случае АВ и АС - наклонные, а ВС - расстояние между ними, которое нужно найти. Проведём из точки А к прямой перпендикуляр АД. АД делит ВС на 2 отрезка ВД и СД, которые являются проекциями наклонных. Так как АВ=ВС, то ∆АВС - равнобедренный и АД также и медиана, которая делит ВС пополам и так как ВС=13см, то

ВД=СД=12÷2=6см