Question

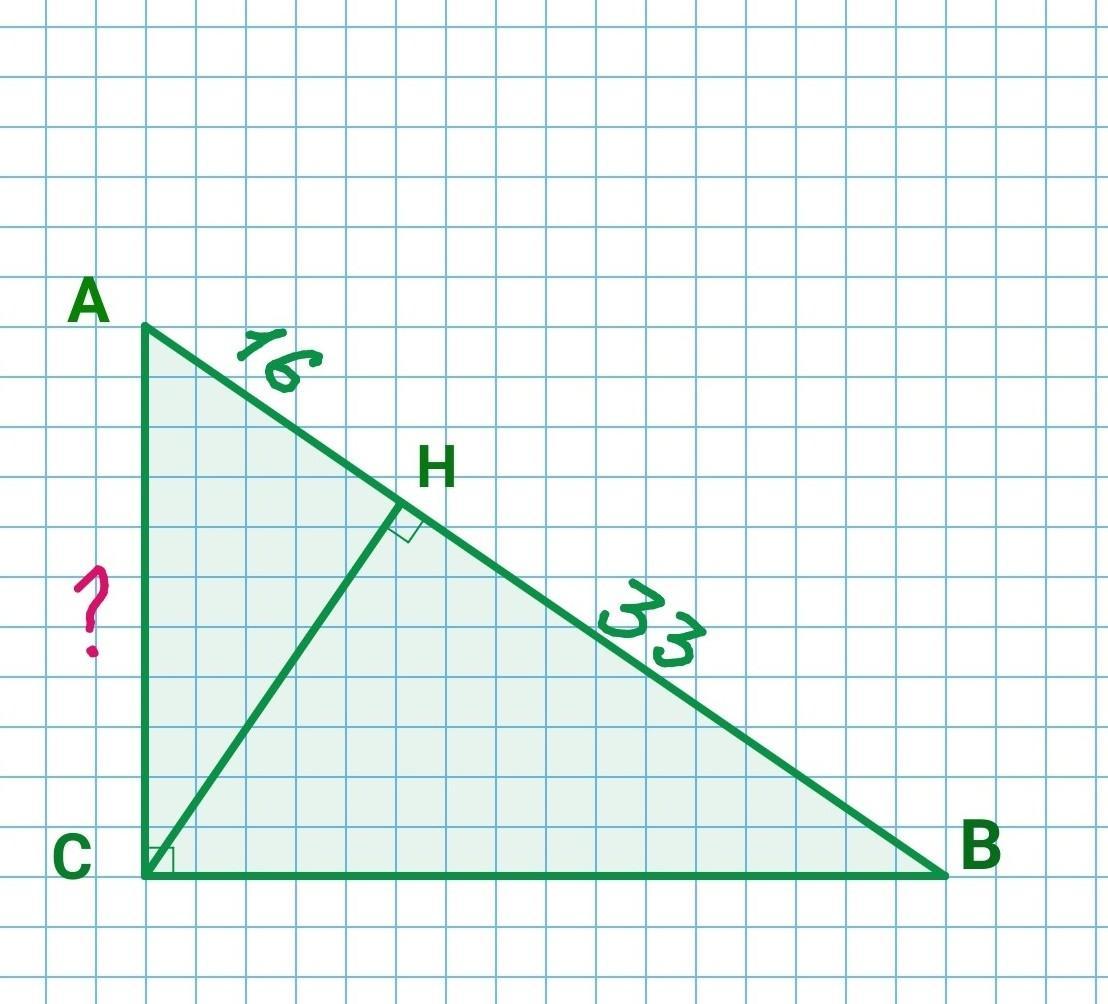
Дано прямокутний трикутник АСВ (кут С прямий), в якому СН - висота.
Проєкції катетів АН та НВ відповідно дорівнюють 16 см та 33 см. Знайдіть
катет АС.

Answer 1

Ответ:

Катет AC дорівнює 28 см

Объяснение:

Дано прямокутний трикутник АСВ (кут С прямий), в якому СН - висота. Проєкції катетів АН та НВ відповідно дорівнюють 16 см та 33 см. Знайдіть катет АС.

• Катет прямокутного трикутника є середнім пропорційним гіпотенузи і проекції цього катета на гіпотенузу, тобто:

$\boxed {\bf {AC}^{2} = AB \cdot AH}$

Дан прямокутний трикутник АВС, AH=16 см, HB=33 см.

Гіпотенуза АВ =АН+НВ=16+33= 49 (см)

Тоді катет АС:

АС²= 49•16

$AC = \sqrt{49\cdot16 } = 7\cdot 4 = \bf 28$ (см)

Відповідь: 28 см

#SPJ1