ДОПОМОЖІТЬ!!!!!!!
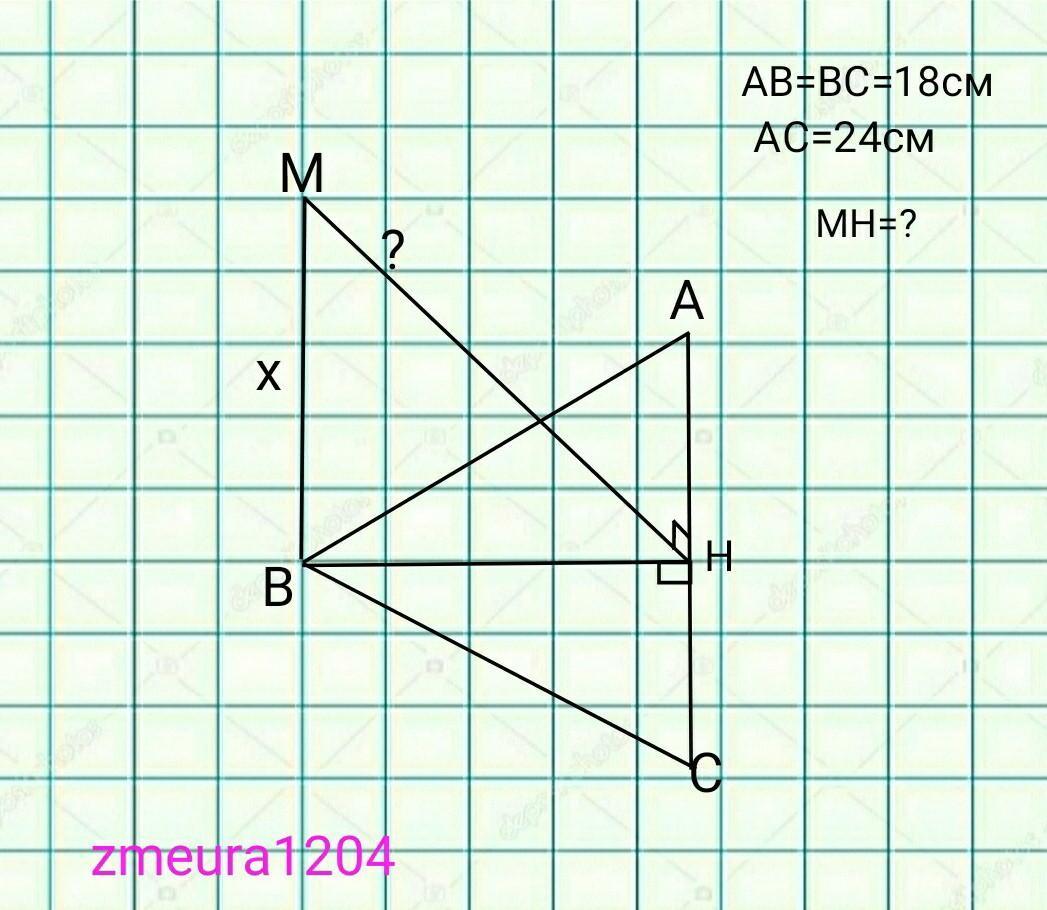
Через вершини в рівнобедреного трикутника АВС (АВ = ВС) проведено пряму ВМ , перпендикулярну до його площини. Обчисліть відстань між прямими ВМ та АС , якщо АВ = 18 см, АС = 24 см.
zmeura1204:
Не стає даних.
ВМ=?
в задачі не напимано скільки ВМ =
Ответы
Ответ дал:
3
Ответ:
Не достатньо даних.
Объяснение:
BH- висота, медіана і бісектриса рівнобедреного трикутника ∆АВС, АВ=ВС, за умови.
АН=СН, ВН- медіана.
АН=АС/2=24/2=12см
∆АВН- прямокутний трикутник.
За теоремою Піфагора:
ВН=√(АВ²-АН²=√(18²-12²)=
=√((18-12)(18+12))=√(6*30)=
=√(2*3*2*3*5)=6√5 см.
ВН перпендикулярно АС, тоді МН перпендикулярно АС, за теоремою о трьох перпендикулярах. Необхідно знайти МН.
Далі не стає даних.
Пояснення
∆ВМН- прямокутний трикутник.
За теоремою Піфагора:
МН²=ВМ²+ВН².
Візьмемо за ВМ=х.
МН=√(х²+(6√5)²)=√(х²+180)
Приложения:
дякуююю
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад