Question

помогите нужно дано с рисунком и решение 8 клас геометрия номер 493 и номер 495 срочно!!!!!! ​ номер 493
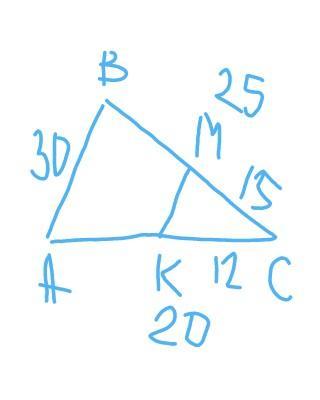
на сторонах АC і ВС трикутника АВС позначили відповідно точки М і К так, що СМ=15 см, СК=12см . знайдіть відрізок МК, якщо АС =20см , ВС=25 см, АВ=30 см
номер 495!
Чи подібні два трикутника, якщо сторони одного відносяться як 3 : 8 : 9 , а сторони другого = 24 см, 9 см, 27 см?

Answer 1

Объяснение:

493.

дано:

∆АВС

К∈АС ; М∈ВС ; СК=12 см; МС=15 см;

АС=20 см; ВС=25 см ; АВ=30 см

Найти: КМ

k - коэффициент подобия

k=AC/CK=BC/CM=20/12=25/15=5/3, значит

∆АВС~∆КМС,∠С общий

k=AB/KM

KM=AB/k=30÷5/3=30•3/5=18 см

495.

дано :

стороны ∆1относятся 3:8:9

стороны ∆2 : 24 см; 9 см; 27 см

найти : ∆1~∆2 ?

решение:

стороны одного треугольника :

3х см ; 8х см ; 9х см

стороны другого треугольника:

24 см; 9 см ; 27 см

k -коэффициет подобия

k=9/3х=24/8х=27/9х=3/x

так как отношение соответствующих сторон двух данных треугольников равны ,то треугольники подобны.