Question

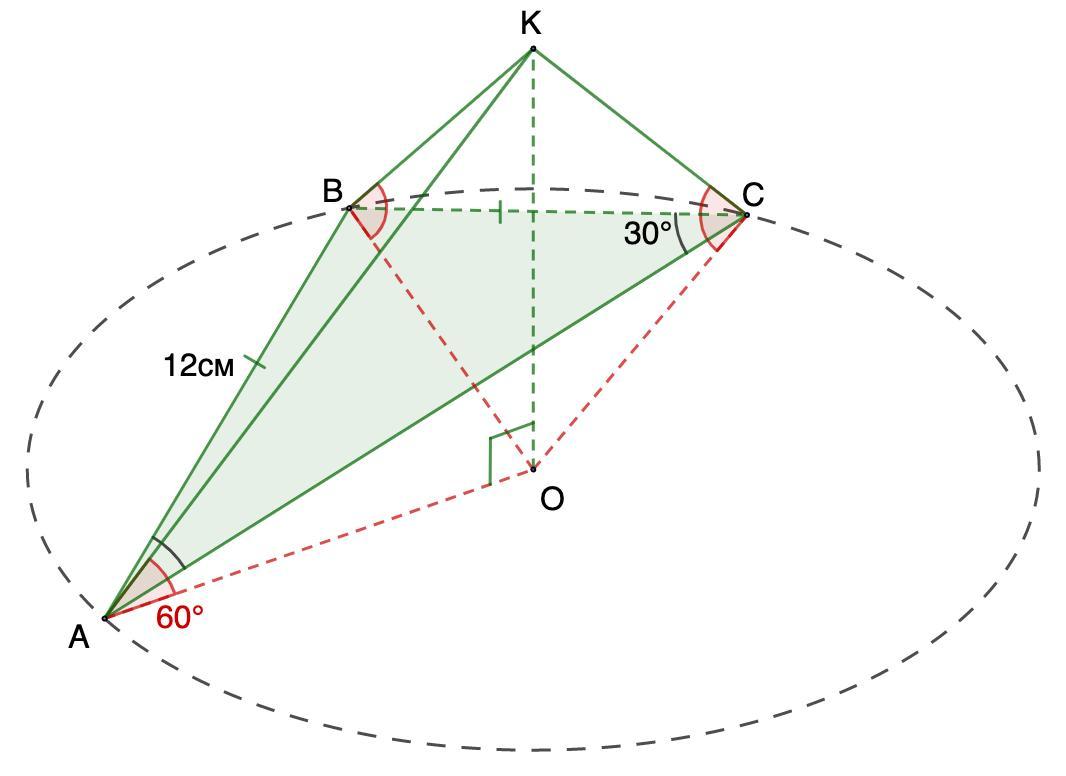
100b)Основою піраміди є рівнобедрений трикутник з кутом 30° при основи і бічною стороною 12 см. Усі бічні ребра піраміди утворюють з площиною основи кут 60°. Знайдіть об'єм піраміди.

Answer 1

Ответ:

Объем пирамиды равен 432 см³.

Пошаговое объяснение:

Основой пирамиды является равнобедренный треугольник с углом 30° при основании и боковой стороной 12 см. Все боковые ребра пирамиды образуют с плоскостью основания угол 60°. Найдите объем пирамиды.

Дано: КАВС - пирамида;

ΔАВС - равнобедренный;

∠ВАС = ∠ВСА = 30°;

АВ = ВС = 12 см;

∠КАО = ∠КВО = КСО = 60°

Найти: V пирамиды

Решение:

• Если все боковые ребра наклонены к плоскости основания под одним и тем же углом, то основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды.

⇒ КО - высота пирамиды.

Объем пирамиды равен:

$\displaystyle \bf V=S_{OCH}\cdot h$

1. Найдем площадь основания.

Рассмотрим ΔАВС - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠ВАС = ∠ВСА = 30°

• Сумма углов треугольника равна 180°.

⇒ ∠АВС = 180° - (30° + 30°) = 120°

Площадь треугольника найдем по формуле:

$\displaystyle \bf S=\frac{1}{2}ab \cdot sin\gamma$,

где a и b - стороны треугольника, γ - угол между ними.

$\displaystyle S(ABC)=\frac{1}{2}AB\cdot BC \cdot sin120^0=\frac{1}{2}\cdot12\cdot12\cdot\frac{\sqrt{3} }{2} =36\sqrt{3}\;_{(CM^2)}$

2. Найдем высоту пирамиды.

Рассмотрим ΔАВО.

АО = ОВ = R

⇒  ΔАВО - равнобедренный.

• Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

∠ВСА = 30° - вписанный.  ⇒ ∠ВОА = 30° · 2 = 60° - центральный.

• Если в равнобедренном треугольнике один из углов равен 60°, то этот треугольник равносторонний.

⇒ АВ = ОА = ОВ = 12 см

Рассмотрим ΔАКО - прямоугольный.

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle tg60^0=\frac{KO}{AO}\\ \\KO=12\cdot \sqrt{3}\;_{(CM)}$

Найдем объем пирамиды:

$\displaystyle V=\frac{1}{3}\cdot 36\sqrt{3} \cdot 12\sqrt{3} =432\;_{(CM^3)}$

Объем пирамиды равен 432 см³.

#SPJ1