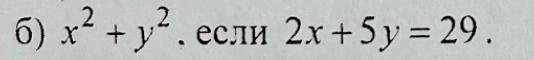Ответы
Ответ дал:
1
Ответ:
Найти наименьшее значение выражения . если
Выразим переменную х из линейного уравнения.
Подставим в заданное выражение.
Получили сумму. Первое слагаемое при любых значениях переменной y неотрицательно, то есть . Второе слагаемое строго больше 0 ,
. Наименьшее значение эта сумма примет в том случае, если первое слагаемое обратиться в 0 . А это возможно при
.
Наименьшее значение выражение равно 29 при условии, что
.
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад