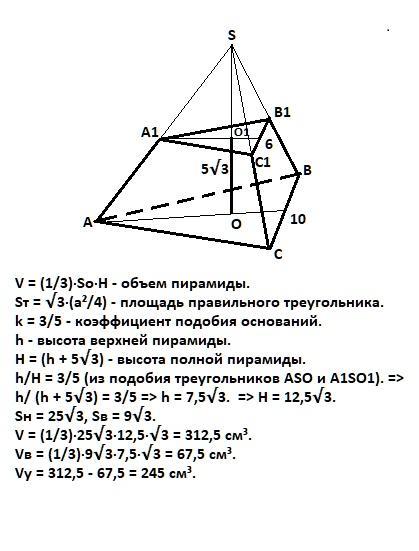
Вычислить Объем правильный усеченной треугольный пирамиды если стороны ее оснований равный 6 см и 10 см а перпендикуляр который соединяет основания равен 5v3
Ответы
Ответ:
V = 245 cм³.
Объяснение:
Пусть была правильная треугольная пирамида SАВС со стороной основания, равной 10 см. Проведем параллельно основанию сечение этой пирамиды на высоте, равной 5∨3 см. Получим данную нам усеченную пирамиду со стороной верхнего основания, равной 6 см.
Объем пирамиды SABC равен V = (1/3)·Sн·H, где Sн - площадь основания, Н - высота пирамиды. Соответственно, объем отсекаемой (верхней) пирамиды SA₁B₁C₁ равен Vв = (1/3)·Sв·h.
Заметим, что Н = h+5∨3.
Правильные треугольники подобны с коэффициентом подобия, равным отношению сторон. => k = 6/10 = 3/5.
Следовательно, основания усеченной пирамиды и все их линейные элементы подобны с этим коэффициентом. =>
Треугольники A₁SO₁ и АSO подобны с k = A₁O₁/АО = 3/5.
Площадь правильного треугольника равна:
S = √3·(a²/4) - формула.
Из всего вышесказанного имеем:
h/(h+5√3) = 3/5. => h = 7,5√3 см. => H = 12,5√3 см.
Sн = 25√3 см²- площадь нижнего основания.
Sв = 9√3 см² - площадь верхнего основания.
Тогда объем полной пирамиды равен:
V = (1/3)·25√3·12,5·√3 = 312,5 см³.
Объем верхней (отсекаемой) пирамиды:
Vв = (1/3)·9√3·7,5·√3 = 67,5 см³.
Объем усеченной пирамиды:
Vу = 312,5 - 67,5 = 245 см³.