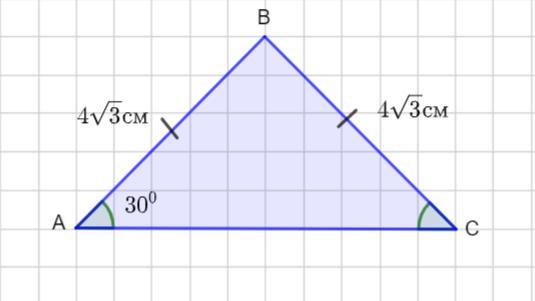
Найдите площадь равнобедренного треугольника с углом при основании 30° и боковой стороной, равной 4√3 см. Полученный ответ поделите на

Ответы
Ответ дал:
2
Ответ:
12.
Объяснение:
Найти площадь равнобедренного треугольника с углом при основании 30° и боковой стороной, равной 4√3 см. Полученный ответ поделите на √3.
Пусть дан ΔАВС - равнобедренный
АВ =ВС = 4√3 см , ∠ А =30 °.
В равнобедренном треугольнике углы при основании равны . Тогда ∠С = ∠А =30°.
Сумма углов треугольника равна 180 °. Тогда ∠В = 180°- ( ∠А +∠С)
∠В =180° - ( 30°+30°) = 180 °- 60° = 120°
Площадь треугольника равна полупроизведению двух сторон на синус угла между ними.
см ².
Значит, площадь треугольника равна 12 √3 см ².
Разделим полученное число на √3 и получим 12.
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад