Question

В равнобедренном прямоугольном треугольнике ABC гипотенузой является сторона
AB=
$6 \sqrt{2}$

найди угол между AB и CB. Ответ дайте в градусах

Найдите AB×CB​

Answer 1

Ответ:

Угол между AB и CB равен 45°

AB·CB = $36\sqrt{2}$

Объяснение:

Нужно знать:

1) В равнобедренном треугольнике углы при основании равны.

2) Сумма острых углов прямоугольного треугольника равна 90°.

3) Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

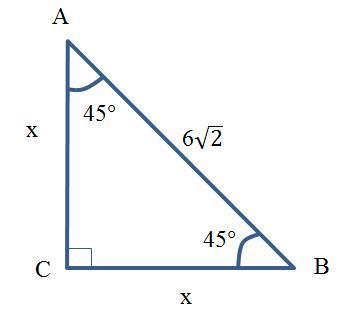
Решение. ABC равнобедренный прямоугольный треугольник (см. рисунок) с равными боковыми сторонами AC и CB. Поэтому основанием будет гипотенуза AB.

Тогда углы при основании AB равны: ∠А = ∠В. Так как сумма острых углов прямоугольного треугольника равна 90°, то каждый из острых углов равен 90°:2 = 45°.

Далее, по теореме Пифагора

AB² = AC² + BC².

Но AC = BC = x, следовательно

$\tt (6\sqrt{2})^2 = x^2+x^2 \\2 \cdot x^2 = 72 \\x^2 = 36 \\ x = 6.$

Теперь можем найти произведение сторон:

AB·CB = $6\sqrt{2} \cdot 6 = 36\sqrt{2}.$

#SPJ1