Ответы
Ответ дал:
1
Ответ:
Подробное решение на фото
Удачи!)
Приложения:
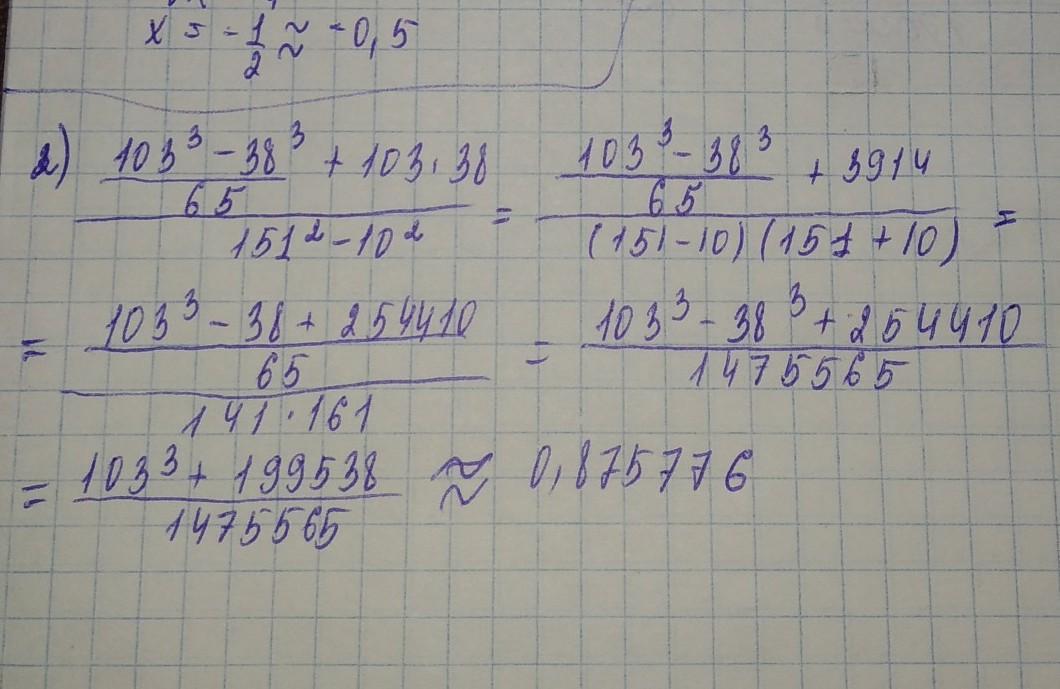
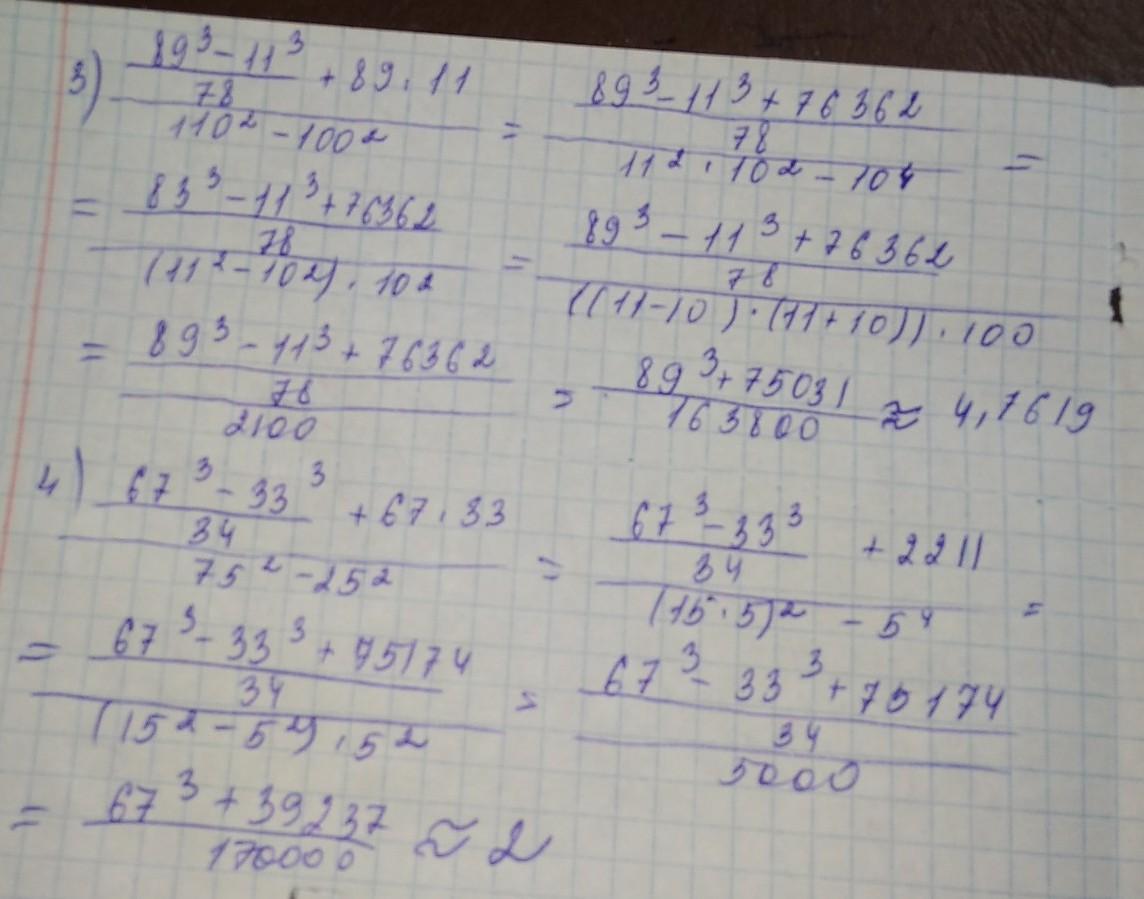
crehimli30cahad:
Спасибо
можете пожалуйста закрепить как лучший ответ?)
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Вычислить:
Для решения надо знать:
a³ - b³ = (a - b)(a² + ab + b²)
a² - b² = (a - b)(a + b)
(a + b)² = a² + 2ab + b²
Спасибо
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
