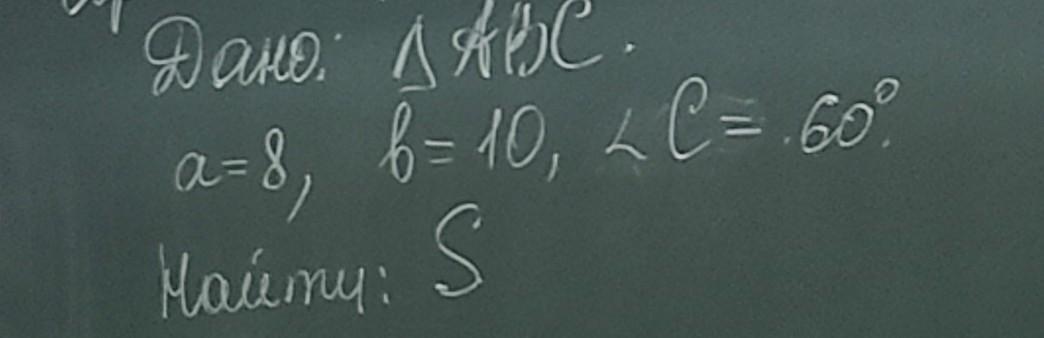Question

Дано: . a=8, b= 10₁ LC = 60° Найти: S​

Answer 1

Извините, возможно я допустил ошибку. Проверим вычисления:

Сначала найдем третью сторону треугольника, используя теорему косинусов:

c^2 = a^2 + b^2 - 2abcos(LC)

c^2 = 8^2 + 10^2 - 2810cos(60°)

c^2 = 164

c ≈ 12.806

Теперь, используя формулу Герона, найдем площадь треугольника:

p = (a + b + c) / 2

S = sqrt(p * (p - a) * (p - b) * (p - c))

где p - полупериметр треугольника.

p = (8 + 10 + 12.806) / 2 = 15.403

S = sqrt(15.403 * (15.403 - 8) * (15.403 - 10) * (15.403 - 12.806)) ≈ 39.17

Таким образом, площадь треугольника с длинами сторон a=8, b=10 и углом между ними LC=60° примерно равна 39.17 квадратных единиц (округленно до двух знаков после запятой). Извините за путаницу и неправильный ответ в прошлый раз.