Question

СРОЧНО 10 МИНУТ ДО КОНЦЯ УРОКА
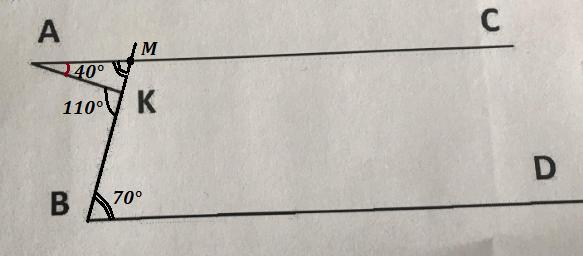
Відомо, що кут КАС = 40° , кут АКБ = 110° , КВД = 70° .Доведіть , що прямі АС і ВД зображені на малюнку паралельні​

Answer 1

Ответ:

Продлим ВК до пересечения с АС в точке М .

Получили ΔАКМ , ∠АКВ - внешний угол этого треугольника ,  

∠АКВ = ∠КАМ + ∠АМК  ⇒  

∠АМК = ∠АКВ - ∠КАМ = 110° - 40° = 70°

∠АМК = ∠КВD = 70°  

Причём ∠АМК  и  ∠КВD  являются внутренними накрест лежащими углами при прямых  АС и BD  и  секущей ВМ . Так как эти углы равны, то прямые АС и BD параллельны ( по признаку параллельности прямых ).

АС || BD , что и требовалось доказать .