Question

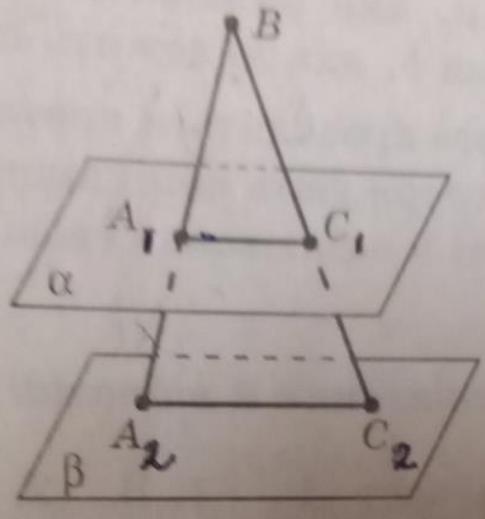
Паралельні площини перетинають сторони кута В у точках А1, С1 і А2, С2 відповідно ( див. мал.). Знайдіть довжину
відрізка ВС2, якщо ВА1 : А1А2 = 1 : 3 і
ВС1 = 3 см.

Answer 1

Ответ:

1 см

Объяснение:

За умовою, ми знаємо, що ВА1 : А1А2 = 1 : 3. Це означає, що А1А2 становить 3/4 всієї довжини сторони В (БА2), тобто А2С2 = 1/4 сторони В.

Оскільки площини паралельні, то А1С1 і А2С2 також паралельні, тому трикутники А1ВС1 та А2ВС2 подібні. Звідси отримуємо наступне співвідношення:

ВС2 / С2А2 = ВС1 / С1А1

Підставляємо відомі значення:

ВС2 / (1/4 ВБ) = 3 см / (3/4 ВБ)

Спрощуємо вираз:

ВС2 = (1/4 ВБ) * (3 см / (3/4 ВБ)) = 1 см

Тому, довжина відрізка ВС2 дорівнює 1 см.