Периметр рівнобедреного трикутника дорівнює 48 см. Знайдіть сторони цього три- кутника, якщо його основа складає 0,4 бічної сторони. можна картінкой.
Ответы
Ответ дал:
2
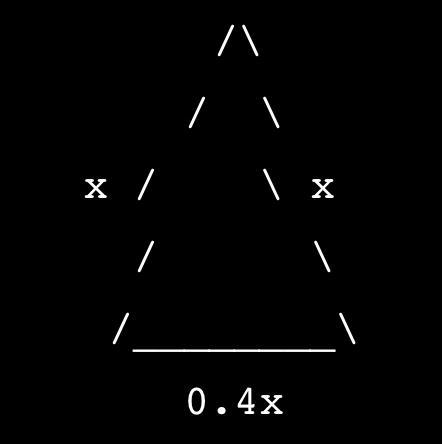
Позначимо бічну сторону рівнобедреного трикутника як x, тоді його основа дорівнюватиме 0.4x.
Оскільки трикутник є рівнобедреним, то його бічні сторони мають однакову довжину. Отже, периметр трикутника складатиметься з основи та двох бічних сторін:
P = x + x + 0.4x = 2.4x
З умови задачі відомо, що периметр трикутника дорівнює 48 см, тому:
2.4x = 48
x = 20
Отже, бічна сторона рівнобедреного трикутника дорівнює 20 см, а його основа має довжину 0.4x = 8 см.
Таким чином, сторони цього трикутника дорівнюють 20 см, 20 см і 8 см. Нижче наведено малюнок рівнобедреного трикутника з відповідними позначеннями:
Оскільки трикутник є рівнобедреним, то його бічні сторони мають однакову довжину. Отже, периметр трикутника складатиметься з основи та двох бічних сторін:
P = x + x + 0.4x = 2.4x
З умови задачі відомо, що периметр трикутника дорівнює 48 см, тому:
2.4x = 48
x = 20
Отже, бічна сторона рівнобедреного трикутника дорівнює 20 см, а його основа має довжину 0.4x = 8 см.
Таким чином, сторони цього трикутника дорівнюють 20 см, 20 см і 8 см. Нижче наведено малюнок рівнобедреного трикутника з відповідними позначеннями:
Приложения:
Ответ дал:
1
Ответ:
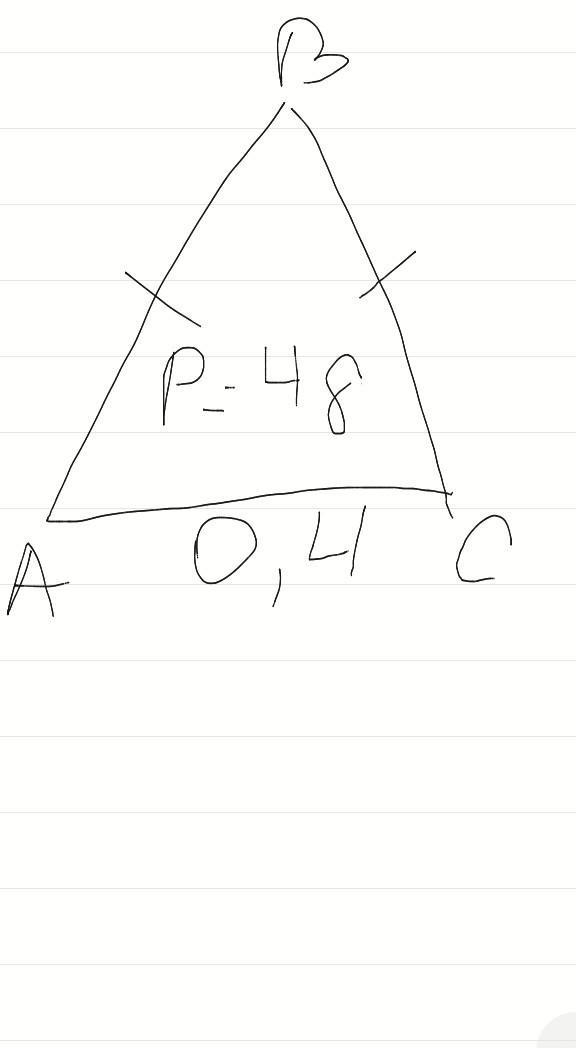
АВ=20 см, ВС= 20см, АС= 8 см
Объяснение:
1)Так як АВС- рівнобедрений трикутник, то його бічні сторони- АВ=ВС, то нехай АВ=ВС=х, тоді АС= 0,4х
2) Р= АВ+ВС+АС
2х+ 0,4х=48
2,4х= 48
х=20
3) АВ=20 см
ВС=20 см
4)АС= 0,4*20= 8см
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
8 лет назад