Острые углы прямоугольного треугольника равны 24 и 66 градусов. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Приложения:
Ответы
Ответ дал:
0
AM=MC.В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы(по теореме) значит, САМ=АСМ.
АСН-АСМ=МСН
66-24=42
АСН-АСМ=МСН
66-24=42
Ответ дал:
0
нет не так
Ответ дал:
0
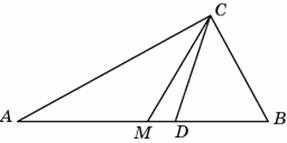
Прямоугольный треугольник АСВ угол С=90, угол А=24, угол В=66
Медиана СМ = 1/2 гипотенузы АВ.
Треугольник АМС равнобедренный, угол А = углу АСМ = 24
Угол АСД = 45 град, СД -биссектриса
угол МСД = 45 - 24 =21 град
Медиана СМ = 1/2 гипотенузы АВ.
Треугольник АМС равнобедренный, угол А = углу АСМ = 24
Угол АСД = 45 град, СД -биссектриса
угол МСД = 45 - 24 =21 град
Ответ дал:
0
вот правельное
Ответ дал:
0
спасибо большое
Ответ дал:
0
ок
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
11 лет назад