ПОМОГИТЕ ПОЖАЛУЙСТА
Укажіть ознаку, за якою можуть бути рівними трикутники АВС і CDA
• A) за двома сторонами і кутом між ними
O B) за трома сторонами
О Б) за стороною і двома прилеглими кутами
О Г) за трьома кутами
Второе зд

Ответы
Відповідь:
1. В)
2. В) (AB = DC, AD = BC – за умовою задачі,
AC – спільна для обох трикутників).
3. Як ми довели в попередньому питанні, ∆ACB = ∆ADC, а у рівних трикутників відповідні сторони і кути рівні, тому ∠BCA = ∠CAD = 20°, так як ∠BCA = 20°, за умовою задачі.
Відповідь: Б) 20°
4. У рівностороннього трикутника всі сторони рівні, тому його периметр можна знайти за формулою:
P∆ = 3a, де a – сторона трикутника.
P∆ = 16,5 см
3a = 16,5
a = 16,5/3
a = 5,5(см).
Відповідь: Г) 5,5 см.
5. Дано: ∆ABC і ∆KMP
∆ABC = ∆KMP, AB = 3 см; BC = 4 см;
P∆abc = 12 см;
Знайти: KP - ?
Розв'язання:
У рівних трикутників відповідні сторони і кути рівні, тому: AB = KM, BC = MP, а AC = KP.
P∆abc = AB + BC + AC
3 + 4 + AC = 12
AC = 12-7
AC = 5(см)
KP = AC = 5 см, як відповідні сторони рівних трикутників ∆ABC і ∆KMP.
Відповідь: Б) 5см.
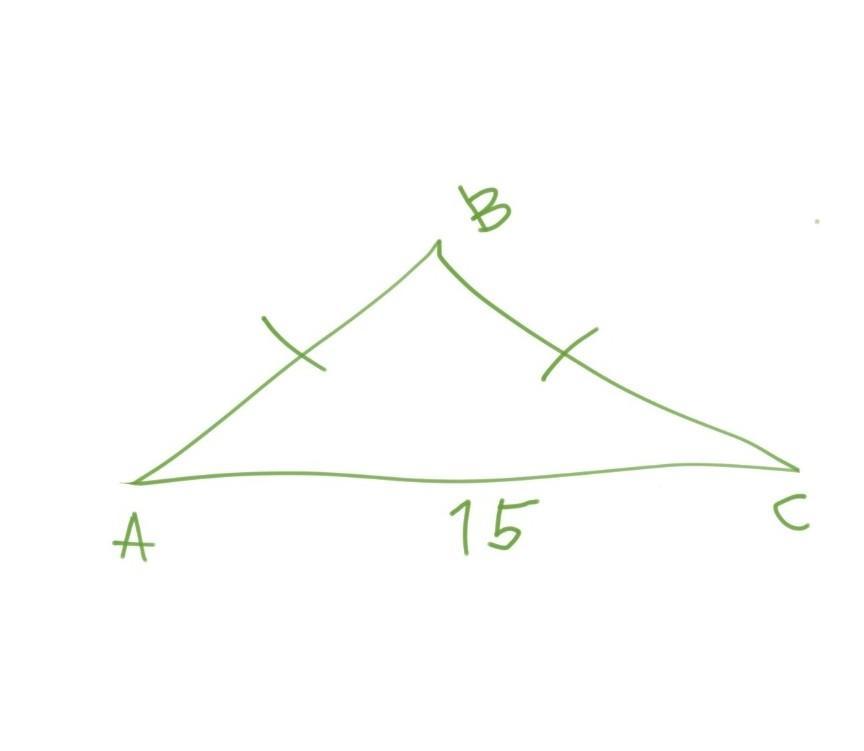
6. Дано: ∆ABC
(Малюнок на закріпленому фото)
AC – основа ∆ABC; AC = 15 см;
AB = BC, на 6 см більші, ніж AC.
Знайти: P∆abc - ?
Розв'язання: P∆abc = AB + BC + AC, але оскільки ∆ABC – рівнобедрений з основою AC, то його периметр можна знайти за формулою:
P∆abc = AC + 2AB
AB = BC = AC+6
AB = BC = 15+6 = 21(см)
P∆abc = 15+2·21 = 15+42 = 57(см)
Відповідь: 57 см.