Question

100БАЛЛОВ, ЗАДАНИЕ НА ФОТО, ОДНО. Спас-Бан.​

Answer 1

Ответ:

Доказано, что высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.

Объяснение:

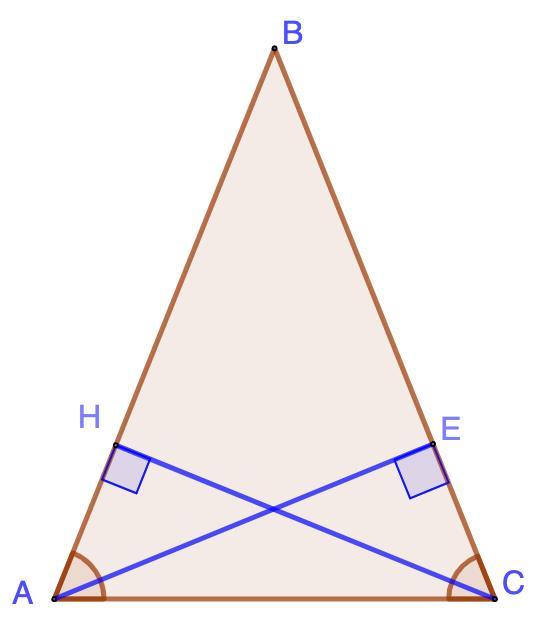
438. Докажите, что высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.

Дано: ΔАВС - равнобедренный;

АЕ и СН - высоты;

Доказать: АЕ = СН.

Доказательство:

ΔАВС - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠А = ∠С

Рассмотрим ΔАНС и ΔАЕС - прямоугольные.

∠А = ∠С; АС - общая.

⇒ ΔАНС = ΔАЕС (по гипотенузе и острому углу)

В равных треугольниках против равных углов лежат равные стороны.

⇒ АЕ = СН.