Допоможіть! Даю 60 балів!
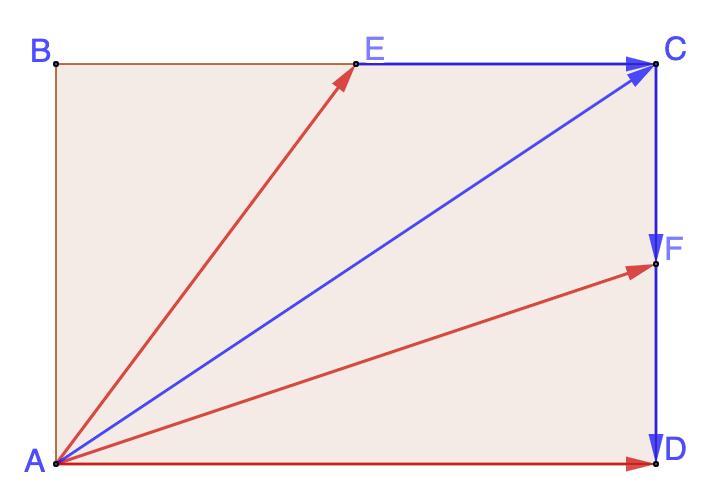
АВСD прямокутник , точки Е і F середини сторін BC та CD відповідно. Виразіть вектор АF через вектори АЕ і AD
Аноним:
так а где файл
щас отвечу
Ответы
Ответ дал:
1
Ответ:
Объяснение:
АВСD прямоугольник, точки Е и F середины сторон BC и CD соответственно. Выразить вектор AF через векторы AE и AD.
Вспомним сложение векторов по правилу треугольника.
- Для сложения двух векторов a и в по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
Проведем диагональ АС.
Воспользуемся правилом сложения векторов.
1. ΔАЕС.
По условию ВЕ = ЕС.
- Противоположные стороны прямоугольника равны.
⇒ ЕС = 1/2 AD
Получим:
(1)
2. ΔACD.
Подставим вместо вектора АС его выражение (1):
3. ΔACF.
(2)
По условию CF = FD
⇒ (3)
Подставим в равенство (2) соответствующие выражения (1) и (3):
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад