Question

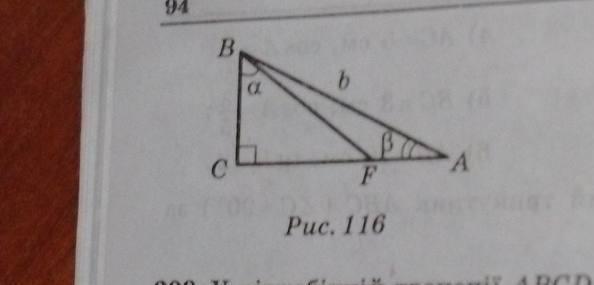
У прямокутному трикутнику ABC, C=90°, AB=b, BAC=бета, FBC=альфа, Знайдіть відрізок AF

Answer 1

Ответ:За теоремою синусів в прямокутному трикутнику ABC:

sin(бета) = AB / AC

або

sin(бета) = b / AC

Також за теоремою синусів в трикутнику BFC:

sin(альфа) = FC / BC

Але BC = AC * cos(бета), тому:

sin(альфа) = FC / (AC * cos(бета))

Так як FC = AF * sin(бета), підставляючи це, отримаємо:

sin(альфа) = AF * sin(бета) / (AC * cos(бета))

Звідси ми можемо виразити AF:

AF = sin(альфа) * AC * cos(бета) / sin(бета)

Отже, відрізок AF дорівнює:

AF = sin(альфа) * AC * cos(бета) / sin(бета)

Пошаговое объяснение:

За теоремою синусів в прямокутному трикутнику ABC:

sin(бета) = AB / AC

або

sin(бета) = b / AC

Також за теоремою синусів в трикутнику BFC:

sin(альфа) = FC / BC

Але BC = AC * cos(бета), тому:

sin(альфа) = FC / (AC * cos(бета))

Так як FC = AF * sin(бета), підставляючи це, отримаємо:

sin(альфа) = AF * sin(бета) / (AC * cos(бета))

Звідси ми можемо виразити AF:

AF = sin(альфа) * AC * cos(бета) / sin(бета)

Отже, відрізок AF дорівнює:

AF = sin(альфа) * AC * cos(бета) / sin(бета)