Добрый вечер, помогите пожалуйста с системой. Я перепробовал и замену и выражал одно через другое никак не получается
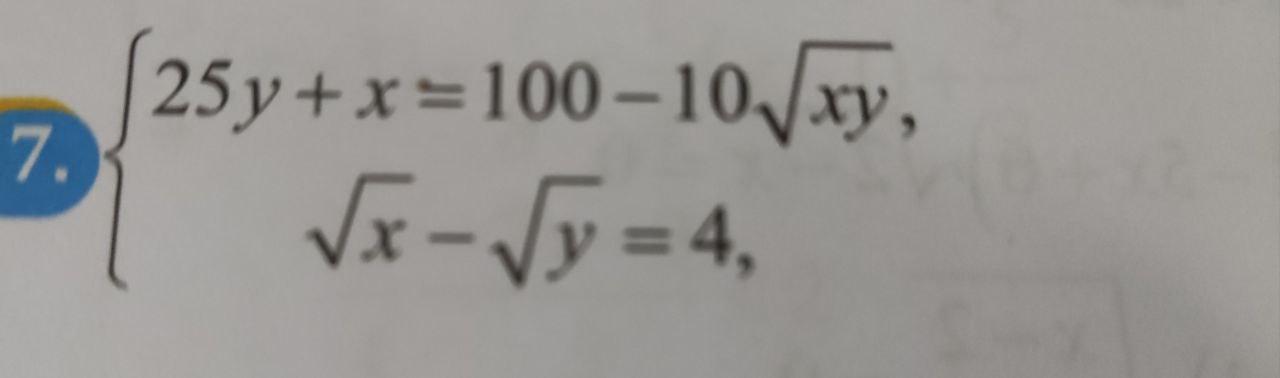
Ответы
Скачайте фотомач, ваша жизнь станет лучшк
Ответ:
Сведем первое уравнение к квадрату, чтобы избавиться от корня:
(25y + x)^2 = (100 - 10√xy)^2
625y^2 + 50xy + x^2 = 10000 - 2000√xy + 100xy
625y^2 - 950xy + x^2 - 10000 = 0 ...(3)
Также, сведем к квадрату второе уравнение:
(√x + √y)^2 = 16
x + 2√xy + y = 16
2√xy = 16 – x – y
4xy = (16 - x - y)^2
4xy = x^2 + y^2 + 256 - 32x - 32y + 2xy
2xy - 32x - 32y + x^2 + y^2 = 256 ...(4)
Итак, имеем систему из двух квадратных уравнений с двумя переменными:
625y^2 – 950xy + x^2 – 10000 = 0
2xy – 32x – 32y + x^2 + y^2 = 256
Решить эту систему можно с помощью подстановок. Подставим во второе уравнение значение √xy из первого уравнения:
2√xy = 2√(100 - 25y - x) = 16 - x - y
4xy = (16 - x - y)^2
2xy – 32x – 32y + x^2 + y^2 = 256
Подставим в последнее уравнение значение 4xy из предыдущего равенства:
(16 - x - y)^2 - 32x - 32y + x^2 + y^2 = 256
256 - 32x - 32y + x^2 + y^2 - 32x - 32y + x^2 + y^2 = 256
2x^2 + 2y^2 - 64x - 64y = 0
x^2 + y^2 - 32x - 32y = 0
x^2 – 32x + y^2 – 32y = 0
(x – 16)^2 + (y – 16)^2 = 256
Итак, имеем круг с центром в точке (16, 16) и радиусом 16. Это означает, что возможно множество решений системы, удовлетворяющих второму уравнению