Question

Точка А лежит на медиане, проведенной к основанию равнобедренного треугольника. Доказать, что она одинаково удалена от вершин основания.

Answer 1

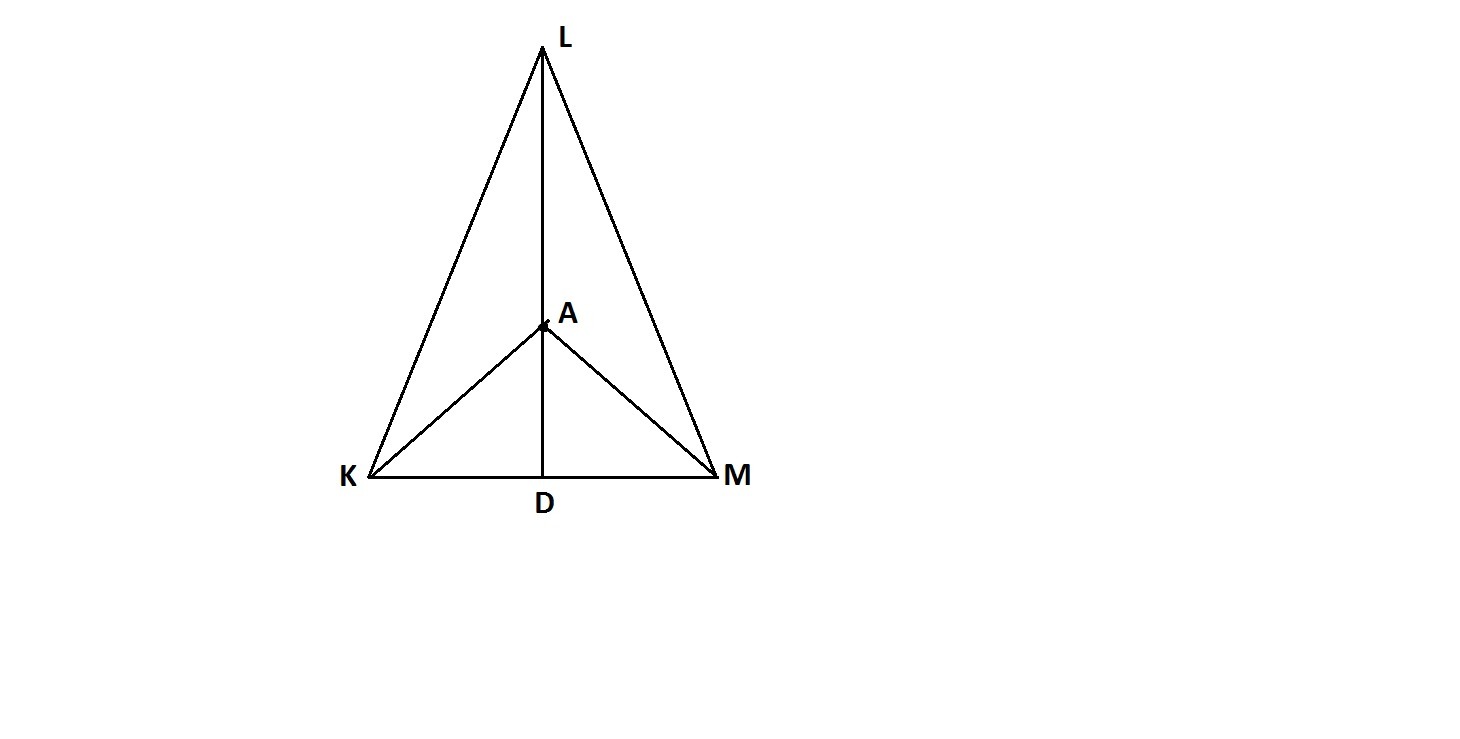
Пусть дан ΔKLM. 
Проведём отрезки AK и AM.
Рассмотрим ΔKAD и ΔMAD.
∠KDA= ∠MDA = 90°, т.к. медиана в равнобедренном треугольнике, проведённая к основанию, является высотой.
KD = DM - т.к. LD - медиана
AD - общий катет
Значит, ΔKAD = ΔMAD - по двум катетам.
Из равенства треугольников ⇒ KA = AM ⇒ точка A равноудалена от вершин основания.