Question

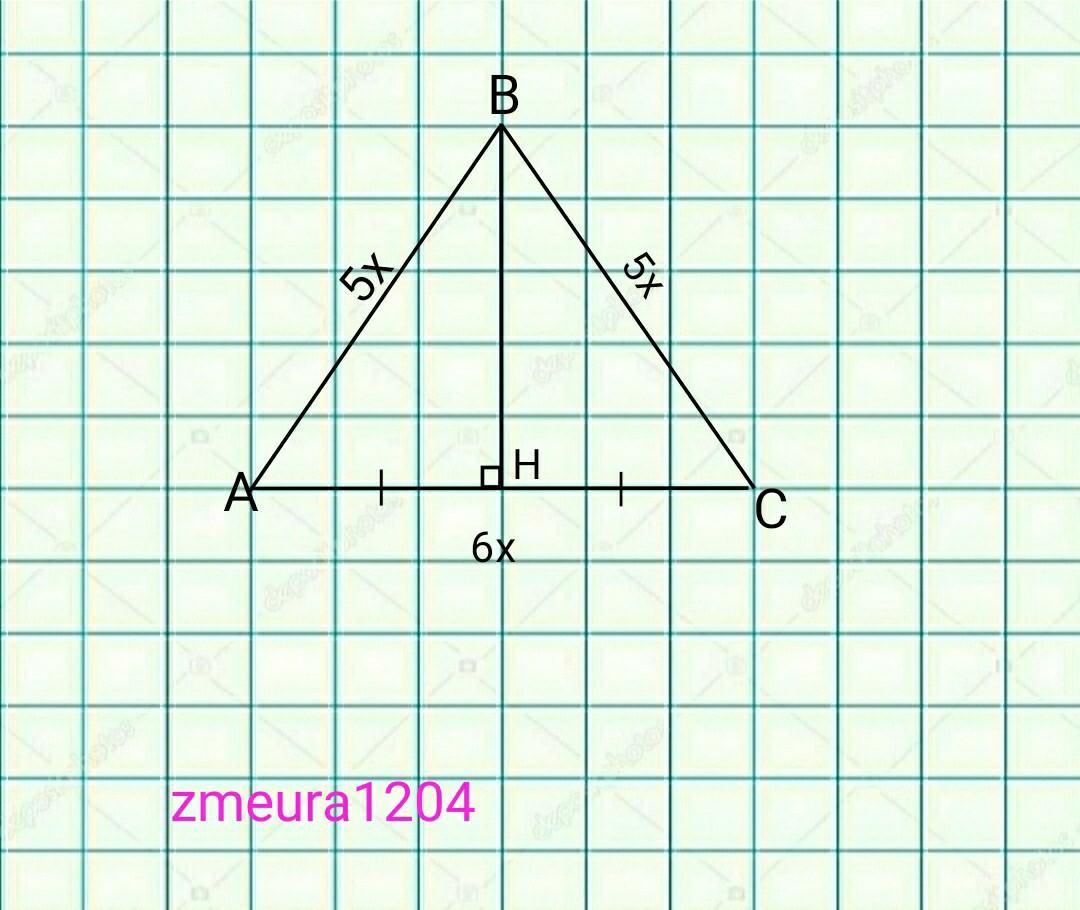
у рівнобедреному трикутнику бічне ребро відноситься до основи як 5:6. Обчисліть периметр цього трикутника якщо довжина описаного кола дорівнює 50п см. Терміново допоможіть

Answer 1

Ответ:

Р(∆АВС)=128см

Объяснение:

C=2πR; → R=C/2π=50π/2π=25 см.

АН=НС, ВН- висота, медіана і бісектриса рівнобедреного трикутника ∆АВС; АВ=ВС.

АН=АС/2=6х/2=3х.

∆АВН- прямокутний трикутник.

За теоремою Піфагора:

ВН=√(АВ²-АН²)=√((5х)²-(3х²))=√(25х²-9х²)=

=√(16х²)=4х.

S∆ABC=½*AC*BH=½*4x*6x=12x².

R=(AB*BC*AC)/(4*S(∆ABC))=(5x*5x*6x)/(4*12x²)=

=150x³/48x²=3,125x.

R=3,125x; R=25см

Рівняння:

3,125х=25

х=25/3,125

х=8

АВ=5х=5*8=40см

ВС=5х=5*8=40см

АС=6х=6*8=48см

Р(∆АВС)=АВ+ВС+АС=40+40+48=128см