Question

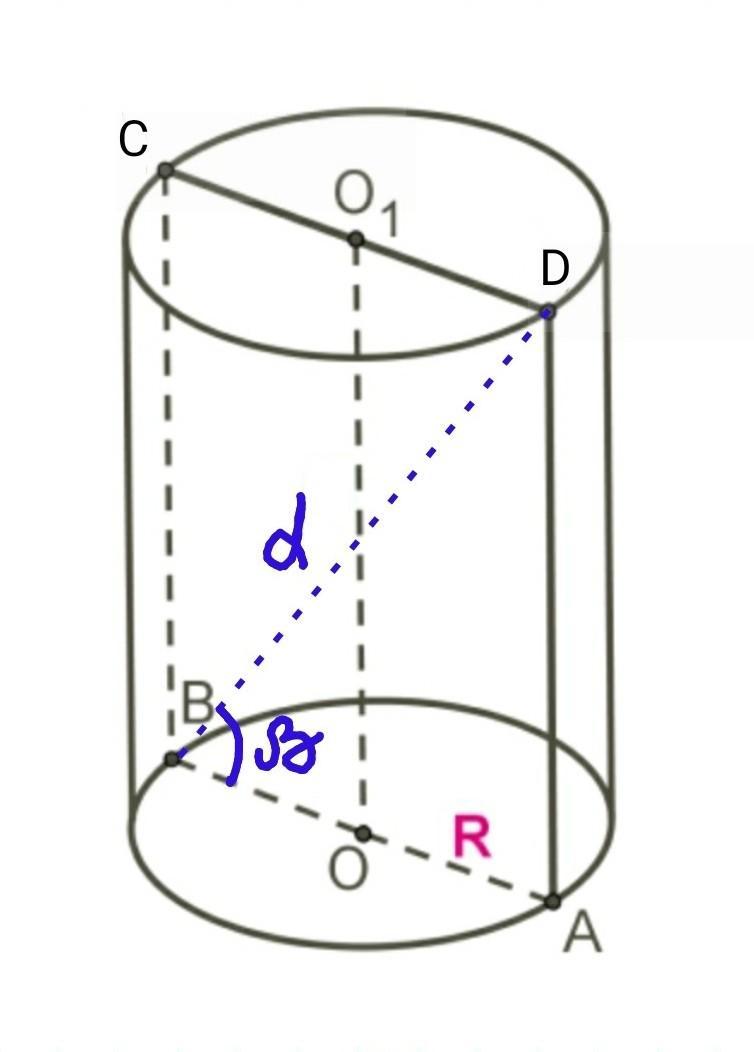
Діагональ осьового перерізу циліндра d i утворює з площиною
основи кут В. Знайти площу основи циліндра

Answer 1

Ответ:

$\bf S = \dfrac{ \pi{d}^{2} }{4} {cos}^{2} \beta$

Объяснение:

Діагональ осьового перерізу циліндра d i утворює з площиною основи кут ß. Знайти площу основи циліндра.

• Переріз циліндра площиною, яка проходить через його вісь, називають осьовим перерізом циліндра.

Осьовим перерізом циліндра є прямокутник ABCD. Сторони BC=AD є твірними циліндра ( їх довжина дорівнює висоті циліндра), а дві інші сторони AB=CD - діаметри ціліндра.

Вісь циліндра ОО1 є віссю прямокутника, і ділить діаметр циліндра навпіл:

АО=ВО=R, R - радіус циліндра.

Діагональ BD (BD=d)прямокутника ABCD ділить його на два прямокутних трикутники. Ортогональною проекцією діагоналі BD є діаметр AB основи циліндра.

Тому кут між діагоналлю BD і площиною основи є кут ABD, отже ∠ABD=ß.

Розглянемо прямокутний трикутник ABD(∠A=90°).

BD = d - гіпотенуза, ∠ABD=ß - кут, що є прилеглим до катета AB.

За означенням косинуса гострого кута прямокутного трикутника маємо:

$\bf \cos \beta = \dfrac{AB}{BD}$

AB=BD•cos ß=d•cos ß

Знаходимо радіус циліндра, як половину діаметра АВ:

$R = \dfrac{AB}{2} = \bf \dfrac{d}{2} \cos \beta$

Оскільки основою циліндра є круг, площа якого дорівнює $\bf \pi {R}^{2}$, то маємо:

$S = \bf \dfrac{\pi {d}^{2} }{4} \cos^{2} \beta$